静态散度校正详解

在大地电磁（MT）和其它频率域电磁勘探方法中，通常要数值求解以下频率域Maxwell方程组：

$$\left\{ \begin{array}{**lr**} \nabla \cdot \sigma E = 0 &\\ \nabla \cdot H = 0 &\\ \nabla \times E = i \omega \mu_0 H &\\ \nabla \times H = \sigma E \end{array} \right.$$

以交错网格有限差分方法为例，对电场旋度方程（法拉第定律）两边取旋度并代入忽略位移电流的磁场旋度方程（麦克斯韦-安培定律），可得到以下有限差分控制方程（双旋度方程）：

$$\nabla \times \nabla \times E = i \omega \mu_0 \sigma E$$

1. 双旋度方程的有限差分线性系统

将双旋度方程在每个单元格按空间方向展开，得到以下三分量耦合方程：

$$\left\{ \begin{array}{**lr**} \frac{\partial^{2} E_x }{ \partial y^{2}} + \frac{\partial^{2} E_x }{ \partial z^{2}} - \frac{\partial^{2} E_y }{ \partial x \partial y} - \frac{\partial^{2} E_z }{ \partial x \partial z} - i \omega \mu_0 \sigma_x E_x = 0 &\\ \frac{\partial^{2} E_y }{ \partial x^{2}} + \frac{\partial^{2} E_y }{ \partial z^{2}} - \frac{\partial^{2} E_x }{ \partial x \partial y} - \frac{\partial^{2} E_z }{ \partial y \partial z} - i \omega \mu_0 \sigma_y E_y = 0 &\\ \frac{\partial^{2} E_z }{ \partial x^{2}} + \frac{\partial^{2} E_z }{ \partial y^{2}} - \frac{\partial^{2} E_x }{ \partial x \partial z} - \frac{\partial^{2} E_y }{ \partial y \partial z} - i \omega \mu_0 \sigma_z E_z= 0 \end{array} \right.$$

上式中$\sigma_x$、$\sigma_y$和$\sigma_z$分别为各向同性电导率在非均匀网格棱边上对不同空间方向的各向异性近似，若电磁场交错采样（如图1），理论上已满足了两个散度条件（Yee, 1966）：

图1 三维MT正演交错网格有限差分各分量差分格式（圆圈表示当前编号的场分量）

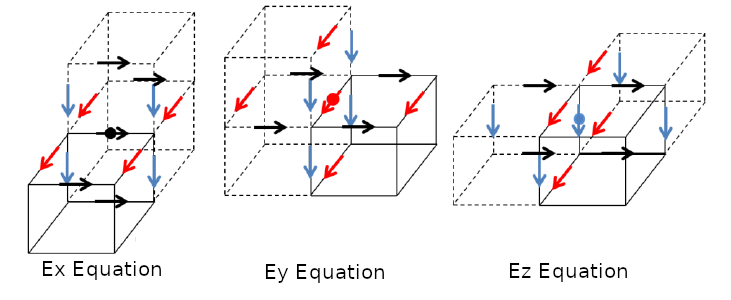
使用差商代替微分，对三维矢量电场$E$经网格编号的待解三维电场向量$e=[e_x, e_y, e_z]^T$及边界条件$b$可得到以下大型稀疏线性方程组：

$$Ke=b$$

若使用直接法（如LU分解，多波前法）等解此线性方程组内存需求巨大，时间和空间复杂度都为$O(n^3)$，因此对于大规模问题，使用Krylov子空间迭代法（如Bicgstab，QMR等）更合适。

2. 静态散度校正的原理

迭代法求解差分方程组时，若模型电导率空间分布函数$\sigma(x,y,z)$非平缓，或者频率非常低的时候收敛速度极慢甚至无法收敛。原因有二：（1）双旋度线性方程组的复系数矩阵$K$在$i \omega \mu_0$很小时非严格主对角占优；（2）当模型复杂时，迭代早期$e_k$会过早拟合$b$的“高频”成分，一旦陷入某个局部奇异解便无法保证整体收敛。（理解第2条需要参考代数多重网格法的原理）。
对于问题（1），需对Krylov子空间迭代施加预条件。选择非耦合部分的标量Helmhoz方程部分作为预条件问题，如下：

$$\left\{ \begin{array}{**lr**} \frac{\partial^{2} E_x }{ \partial y^{2}} + \frac{\partial^{2} E_x }{ \partial z^{2}} + i \omega \mu_0 \sigma_x = 0 &\\ \frac{\partial^{2} E_y }{ \partial x^{2}} + \frac{\partial^{2} E_y }{ \partial z^{2}} + i \omega \mu_0 \sigma_y = 0 &\\ \frac{\partial^{2} E_z }{ \partial x^{2}} + \frac{\partial^{2} E_z }{ \partial y^{2}} + i \omega \mu_0 \sigma_z = 0 \end{array} \right.$$

预条件的本质是把条件数不好的$Ke=b$转换为$MKe=Mb$来求解，其中$M$为上式左边的离散算子矩阵，解$Mv=u$需使用不完全分解+回代方法，经测试不完全Cholesky分解(ICC)和不完全LU分解（ILU）均可大幅提高收敛效率，但模型复杂时无填充的ICC(0)和ILU(0)效果仍然不好（现在MT正演领域没人测试这个），从内存管理和编码实用性来说，带填充的ILU(k)分解性价比相对最高（k=8）。
对于问题(2)，则需用到静态散度校正技术（smith，1996）。若$e_k$为迭代早期满足残差$r_k=K e_k - b$的当前解。因为$e_k$本身并不满足$K e_k = b$，且$r_k$的“高频”成分过多。
若$e_k = e^c_k + e^r_k$，$e^c_k$即为满足电流密度散度为0的部分（对应“低频”成分），$e^r_k$是不满足散度条件的“高频”成分。在第$k$次迭代只保留$e^c_k$即可避免迭代陷入奇异解而极大加速收敛速度。
考虑电场散度条件的连续性问题，且设$E_k=E^c_k+E^r_k$，下式成立：

$$\left\{ \begin{array}{**lr**} \nabla \cdot \sigma E^c_k = 0 &\\ \nabla \cdot \sigma E_k = \nabla \cdot \sigma E^c_k + \nabla \cdot \sigma E^r_k = \nabla \cdot \sigma E^r_k &\\ \end{array} \right.$$

引入标量势$\varphi_k$满足$E^r_k = \nabla \varphi_k$，并代入以上方程，则可得到：

$$\nabla \cdot \sigma \nabla \varphi_k = \nabla \cdot \sigma E_k$$

对$\nabla \cdot \sigma \nabla$算子离散化，可得到以下新线性方程组：

$$D p = c$$

其中向量$p$为$\varphi_k$的离散向量，右端项$c$是对$e_k$应用$\nabla \cdot \sigma$离散算子得到的向量。向量$p$的采样点位于每个长方体单元的节点处，差分算子及采样方式如下图所示：

图2 静态散度校正对标量势的离散二阶算子差分格式（注：黑圈为标量势采样点，箭头为形成右端项的各场分量）

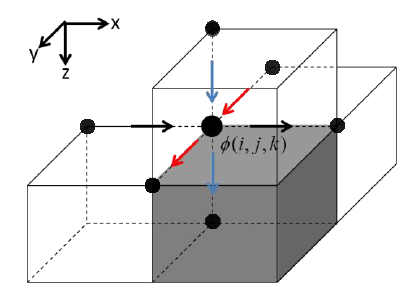
求解方程组$Dp=c$得到$p$之后，对$p$应用离散梯度算子即可得到需校正的$E^r_k$。

3. 带静态散度校正的迭代法

电场双旋度方程的静态散度校正迭代解法流程如下：
(1) $e := 0$
(2) $for \space\space i = 1,..., N$
(3)   求相对拟合差$res:={||b-Ke||}_2 / {||b||}_2$，若小于$10^{-8}$则跳出循环
(4)   常规SQMR或Bicgstab迭代$M$次得到新的$e$
(5)   $for \space\space j = 1,..., L$ (一般$L=5$即可)
(6)     计算向量$c:=Ve$， 其中$V$为算子$\nabla \cdot \sigma$的离散矩阵形式
(7)     计算$div={||c||}_2$，若小于$10^{-10}$则跳出$(1,...,L)$循环
(8)     求解$Dp=c$得到$p$
(9)     更新$e := e - Gp$，其中$G$为离散梯度算子矩阵

以上流程里求解$Dp=c$也是一个耗时过程，如果使用迭代法，单次迭代耗时大致为求解$Ke=b$的⅓。所以内部$Ke=b$的迭代次数$M$和外部循环次数$N$的选择是算法快慢的关键。通过大量模型实验，取$M=100$和$N=20$一般是耗时最短的。不同组合的实验收敛曲线见下图。

图3 用Bicgstab解法不同的循环组合次数的收敛效果对比（注：圆圈表示施加散度校正，灰色M=2，黑色M=10，蓝色M=50，红色M=100，绿色M=200）

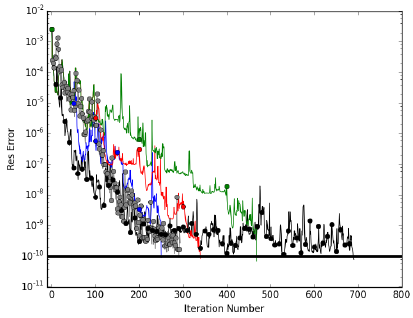
虽然图3显示$M=50$(蓝色)的$Ke=b$的迭代次数最少，但由于求解$Dp=c$的次数是$M=100$（红色）的两倍，总耗时最短的却是$M=100$。

总而言之，静态散度校正是求解低频复杂介质扩散场双旋度方程的迭代法必要过程。究竟多少次$Ke=b$迭代施加一次散度校正是一个trade off，目前还没有最佳的理论方案。