大地电磁阻抗计算及思考
大地电磁(MT)是一种天然源远场平面波勘探方法,利用地面观测的正交水平电磁场定义大地介质的本征电物理参数——阻抗(impedance)。
考虑地下电阻率为水平层状的最简单情况(图1所示的一维介质),对某个频率\omega对应的简谐电磁场复频谱E_x和H_y,阻抗z可以定义为二者之比(标量阻抗)。
由于MT的场源是天然、时变且不可测量的,设某个时段的场源磁距为IL^2,观测场可表示为E_x= C E_x^0和H_x= C H_x^0(其中上标0表示单位场源响应,C是和场源强度有关的量),故有以下关系:
z= \frac{E_x}{H_y} = \frac{E^0_x} {H^0_y}
由上式可知,z扣除了场源时变因素,是只和介质电性有关的物理量。
特别的,当地下介质为一维介质时,无论观测系统的x和y方向如何,在任何观测方位角上的标量阻抗均相同。但除了大型沉积盆地,实际的大地介质均非如此,所以MT方法需观测沿NS和EW两个正交方向的四个电磁场分量[E_x,E_y,H_x,H_y],如下图:
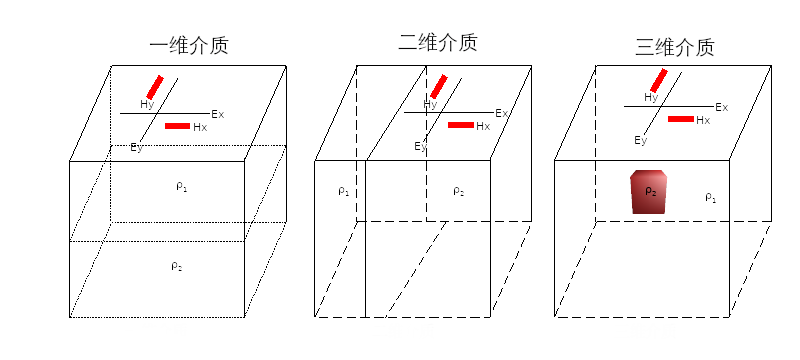
图1 不同维性的大地介质简图
1. 大地电磁张量阻抗
若按正交电磁场频谱的标量阻抗定义,对于非一维介质,在MT观测数据中,至少有互不相同的两个标量阻抗如下:
\left\{
\begin{array}{**lr**}
z_{xy} = \frac {E_x} {H_y} &\\
z_{yx} = \frac {E_y} {H_x}
\end{array}
\right.
也就是说,某个频率\omega的阻抗这一本征物理参数在观测空间域是“各向异性”的。物理上这种“各向异性”需用张量表示(注意:这里的各向异性是“数据空间”的性质,不能和“各向异性介质”混淆)。
由于观测点始终在地面,这种各向异性只发生在(x,y)二维空间内,故张量阻抗形式上是2*2的矩阵。考虑最一般的三维介质情况,它和观测电磁场四个水平分量满足以下关系:
{\begin{bmatrix}
{E_x } \\
{E_y }
\end{bmatrix}}
=
{\begin{bmatrix}
{z_{xx} } & {z_{xy} } \\
{z_{yx} } & {z_{yy} }
\end{bmatrix}}
{\begin{bmatrix}
{H_x } \\
{H_y }
\end{bmatrix}}
上式也可用矩阵形式简记为\boldsymbol{e} = \boldsymbol{Z} \boldsymbol{h},将大地视为一个滤波器,从信号与系统来理解,\boldsymbol{Z}为大地滤波器的传输函数,其反傅里叶变换为系统冲激响应。
可以不严谨的这样理解:输入傅里叶变换为\boldsymbol{h}向量的磁场信号,大地滤波器的输出信号的傅里叶变换为\boldsymbol{e}向量。
标量阻抗的定义损失了介质的维性信息。张量阻抗用统一的形式描述了图1所示的三种介质。对于一维介质,有以下形式:
{\boldsymbol{Z}_{1d}}=
{\begin{bmatrix}
{0 } & {z_{xy} } \\
{z_{yx} } & {0 }
\end{bmatrix}}, \quad where \ z_{xy}=-{z_{yx}}
上式中对z_{yx}取反由电磁感应左手坐标系决定。特别的,当时谐因子取e^{i \omega t}时z_{xy}的实部和虚部均为正数,标准大地电磁仪器均按此标准(不按此标准的MT仪器可认为“不专业”,嘿嘿)。
对于二维介质,张量阻抗为:
{\boldsymbol{Z}_{2d}}=
{\begin{bmatrix}
{0 } & {z_{xy} } \\
{z_{yx} } & {0 }
\end{bmatrix}}, \quad where \ z_{xy} \not=-{z_{yx}}
对于三维介质,张量阻抗的四个元素互不相同。阻抗张量满足旋转操作,将正南北观测的\boldsymbol{Z}^0旋转到方位角为\theta的观测系统时可用下式计算:
{\boldsymbol{Z}^{\theta}}
=
{\boldsymbol{R}} {\boldsymbol{Z}^{0}} {\boldsymbol{R}^{T}},
\quad where \ {\boldsymbol{R}}
=
{\begin{bmatrix}
{cos \theta } & { sin \theta } \\
{-sin \theta } & { cos \theta }
\end{bmatrix}}
很多人对二维介质有可能存在误解。即使是图1中的二维介质,在做二维反演时,维性是和观测角度和测线方位有关的。思考以下几种情况:
1. 如果测线方位角15度,观测方位角和图示一样。二维反演的点距是否要进行角度投影?
2. 如果测线方位角15度,观测方位角也是15度,是否转阻抗?是否点距要进行角度投影?
3. 如果测线方位角是0度,是否能用二维反演恢复模型?
无论如何,图1的二维介质如果观测系统方位角为15度,在新坐标系下的阻抗是三维的。二维反演之前需要找到一个方位角,使得此角度下定义的张量阻抗满足二维介质的阻抗特征,然后才能进行二维反演。
在MT维性分析(一种定性分析手段)里的“二维性”的意思是:可以找到一个确定的观测方位角{\theta},使得z^{\theta}_{xx}和z^{\theta}_{yy}最小(按某种标准判断“小”),且这样的角度在[0,2 \pi]之间只有\theta、\theta+\pi / 2、\theta+\pi和\theta + 3 \pi / 2四个(有明确的90度模糊性电性主轴)。
小贴士: 一维介质和强三维介质没有明确的电性主轴角。
MT数值计算理论里的“二维正演”是说电阻率沿y的方向导数不为0(x为正演剖面方向)。图1中的二维介质如果观测了一条方位角为45度的测线,剖面各测点距为实际点距,此时用二维正演算法无法准确计算MT张量阻抗(点距做角度投影后才能计算准确),当然更直接的方法是三维正演。
所以,MT方法里的“二维介质”这个术语的确切意思需结合上下文理解,它可能表示介质有一个完美的主轴方位,也可能表示当前模型模型参数在垂直剖面方向上的偏导数为0。需要同时理解正演算法和维性分析才可能不出洋相。
小贴士: 思考一下这个表述——该测点在900到1000号测点之间显示强二维性,张量阻抗旋转到20度之后满足二维介质假设。
2. 张量阻抗的最小二乘解与功率谱矩阵
无法直接根据方程\boldsymbol{e} = \boldsymbol{Z} \boldsymbol{h}得到张量阻抗\boldsymbol{Z}的定解,需引入额外的场向量\boldsymbol r(称为参考道)来形成定解方程\boldsymbol{e} \boldsymbol{r}^H = \boldsymbol{Z} \boldsymbol{h} \boldsymbol{r}^H(上标H表示共轭转置)。此时\boldsymbol{Z}为原系统的一个最小二乘解。写成分量形式如下(注意,这里取共轭是为了互相关的噪音压制特性):
{\begin{bmatrix}
{E_x} \\ { E_y }
\end{bmatrix}}
{\begin{bmatrix}
{R_x^* } & { R_y^* }
\end{bmatrix}}
=
{\begin{bmatrix}
{E_x R_x^*} & {E_x R_y^*} \\
{E_y R_x^*} & {E_y R_y^*}
\end{bmatrix}}
=
{\boldsymbol{Z}}
{\begin{bmatrix}
{H_x R_x^*} & {H_x R_y^*} \\
{H_y R_x^*} & {H_y R_y^*}
\end{bmatrix}}
其中,上标*表示取共轭,\boldsymbol{Z}的矩阵形式为:
{\boldsymbol{Z}}
=
{\begin{bmatrix}
{z_{xx}} & {z_{xy}} \\
{z_{yx}} & {z_{yy}}
\end{bmatrix}}
=
{\begin{bmatrix}
{E_x R_x^*} & {E_x R_y^*} \\
{E_y R_x^*} & {E_y R_y^*}
\end{bmatrix}}
{\begin{bmatrix}
{H_x R_x^*} & {H_x R_y^*} \\
{H_y R_x^*} & {H_y R_y^*}
\end{bmatrix}}^{-1}
对于实测数据,某个频率的阻抗需要用电磁场互相关(频率域的共轭乘积)功率谱来表示。首先把时间序列分成N个时窗进行FT变换,然后把该频率不同时窗的的电磁场频谱(一个复数)的乘积求平均,
最后代入阻抗计算公式得到各分量表达式:
\left\{
\begin{array}{**lr**}
z_{xx} = \frac { \overline{ E_x R_x^* }
\overline{ H_y R_y^* }
- \overline{ E_x R_y^* }
\overline{ H_y R_x^* } }
{ \overline{ H_x R_x^* }
\overline{ H_y R_y^* }
- \overline{ H_x R_y^* }
\overline{ H_y R_x^* } } &\\
z_{xy} = \frac { \overline{ E_x R_y^* }
\overline{ H_x R_x^* }
- \overline{ E_x R_x^* }
\overline{ H_x R_y^* } }
{ \overline{ H_x R_x^* }
\overline{ H_y R_y^* }
- \overline{ H_x R_y^* }
\overline{ H_y R_x^* } } &\\
z_{yx} = \frac { \overline{ E_y R_x^* }
\overline{ H_y R_y^* }
- \overline{ E_y R_y^* }
\overline{ H_y R_x^* } }
{ \overline{ H_x R_x^* }
\overline{ H_y R_y^* }
- \overline{ H_x R_y^* }
\overline{ H_y R_x^* } } &\\
z_{yy} = \frac { \overline{ E_y R_y^* }
\overline{ H_x R_x^* }
- \overline{ E_y R_x^* }
\overline{ H_x R_y^* } }
{ \overline{ H_x R_x^* }
\overline{ H_y R_y^* }
- \overline{ H_x R_y^* }
\overline{ H_y R_x^* } }
\end{array}
\right.
上式中每对电磁场上方的横线表示平均互相关功率谱(crosspower)。实际工作中还要根据叠加结果对所有时窗的功率谱进行robust筛选、人工挑选。假设原N个功率谱叠经筛选后只剩下了M个“较好”的,那么M个时窗的叠后7*7功率谱矩阵(增加了和倾子相关的H_z分量,求阻抗只需要6*6矩阵)如下所示:
{\begin{bmatrix}
{\overline{ H_x H_x^* }} & {\overline{ H_x H_y^* }} & {\overline{ H_x H_z^* }} &
{\overline{ H_x E_x^* }} & {\overline{ H_x E_y^* }} &
{\overline{ H_x R_x^* }} & {\overline{ H_x R_y^* }} &\\
{\overline{ H_y H_x^* }} & {\overline{ H_y H_y^* }} & {\overline{ H_y H_z^* }} &
{\overline{ H_y E_x^* }} & {\overline{ H_y E_y^* }} &
{\overline{ H_y R_x^* }} & {\overline{ H_y R_y^* }} &\\
{\overline{ H_z H_x^* }} & {\overline{ H_z H_y^* }} & {\overline{ H_z H_z^* }} &
{\overline{ H_z E_x^* }} & {\overline{ H_z E_y^* }} &
{\overline{ H_z R_x^* }} & {\overline{ H_z R_y^* }} &\\
{\overline{ E_x H_x^* }} & {\overline{ E_x H_y^* }} & {\overline{ E_x H_z^* }} &
{\overline{ E_x E_x^* }} & {\overline{ E_x E_y^* }} &
{\overline{ E_x R_x^* }} & {\overline{ E_x R_y^* }} &\\
{\overline{ E_y H_x^* }} & {\overline{ E_y H_y^* }} & {\overline{ E_y H_z^* }} &
{\overline{ E_y E_x^* }} & {\overline{ E_y E_y^* }} &
{\overline{ E_y R_x^* }} & {\overline{ E_y R_y^* }} &\\
{\overline{ R_x H_x^* }} & {\overline{ R_x H_y^* }} & {\overline{ R_x H_z^* }} &
{\overline{ R_x E_x^* }} & {\overline{ R_x E_y^* }} &
{\overline{ R_x R_x^* }} & {\overline{ R_x R_y^* }} &\\
{\overline{ R_y H_x^* }} & {\overline{ R_y H_y^* }} & {\overline{ R_x H_z^* }} &
{\overline{ R_y E_x^* }} & {\overline{ R_y E_y^* }} &
{\overline{ R_y R_x^* }} & {\overline{ R_y R_y^* }} &\\
\end{bmatrix}}
功率谱矩阵是主对角为实数(自相关)的复共轭对称阵,可用double型数组节省一半存储空间。在SEG标准edi格式>SPECTRA字段里,数组的存储方式如下所示(电-电、电-磁、磁-磁的功率谱单位分别为(mV/km)^2 / Hz、(mV/km) nT / Hz和(nT)^2 / Hz,下标Re和Im分别表示取实部和虚部):
{\begin{bmatrix}
{\overline{ H_x H_x^* }} & {\overline{ H_x H_y^* }}_{Im} & {\overline{ H_x H_z^* }}_{Im} &
{\overline{ H_x E_x^* }}_{Im} & {\overline{ H_x E_y^* }}_{Im} &
{\overline{ H_x R_x^* }}_{Im} & {\overline{ H_x R_y^* }}_{Im} &\\
{\overline{ H_y H_x^* }}_{Re} & {\overline{ H_y H_y^* }} & {\overline{ H_y H_z^* }}_{Im} &
{\overline{ H_y E_x^* }}_{Im} & {\overline{ H_y E_y^* }}_{Im} &
{\overline{ H_y R_x^* }}_{Im} & {\overline{ H_y R_y^* }}_{Im} &\\
{\overline{ H_z H_x^* }}_{Re} & {\overline{ H_z H_y^* }}_{Re} & {\overline{ H_z H_z^* }} &
{\overline{ H_z E_x^* }}_{Im} & {\overline{ H_z E_y^* }}_{Im} &
{\overline{ H_z R_x^* }}_{Im} & {\overline{ H_z R_y^* }}_{Im} &\\
{\overline{ E_x H_x^* }}_{Re} & {\overline{ E_x H_y^* }}_{Re} & {\overline{ E_x H_z^* }}_{Re} &
{\overline{ E_x E_x^* }} & {\overline{ E_x E_y^* }}_{im} &
{\overline{ E_x R_x^* }}_{Im} & {\overline{ E_x R_y^* }}_{Im} &\\
{\overline{ E_y H_x^* }}_{Re} & {\overline{ E_y H_y^* }}_{Re} & {\overline{ E_y H_z^* }}_{Re} &
{\overline{ E_y E_x^* }}_{Re} & {\overline{ E_y E_y^* }} &
{\overline{ E_y R_x^* }}_{Im} & {\overline{ E_y R_y^* }}_{Im} &\\
{\overline{ R_x H_x^* }}_{Re} & {\overline{ R_x H_y^* }}_{Re} & {\overline{ R_x H_z^* }}_{Re} &
{\overline{ R_x E_x^* }}_{Re} & {\overline{ R_x E_y^* }}_{Re} &
{\overline{ R_x R_x^* }} & {\overline{ R_x R_y^* }}_{Im} &\\
{\overline{ R_y H_x^* }}_{Re} & {\overline{ R_y H_y^* }}_{Re} & {\overline{ R_x H_z^* }}_{Re} &
{\overline{ R_y E_x^* }}_{Re} & {\overline{ R_y E_y^* }}_{Re} &
{\overline{ R_y R_x^* }}_{Re} & {\overline{ R_y R_y^* }} &\\
\end{bmatrix}}
将以上实矩阵的各元素代入前文的张量阻抗最小二乘解公式(注意共轭的顺序)即可快速求得张量阻抗的四个元素。
另外,为了估计方差,edi文件还需要在每个频率的7*7矩阵前面存储以下块信息头(假设某edi文件有40个频率,当前频率为320,功率谱矩阵未经旋转,参与叠加的时窗数M=1430):
>SPECTRA FREQ=320.0 ROTSPEC=0.0 AVGT=1430.0 //40
小贴士:只要看一眼功率谱edi文件>SPECTRA字段各矩阵的最后两列是否有0值,就可判断数据处理有无使用远参考道,这对于MT数据验收人员或监理人员是很有用的小知识。思考以下,为什么?:)
3.方差矩阵
阻抗张量的最小二乘解可统一写为 \boldsymbol{Z} = \boldsymbol{e} \boldsymbol{r}^H (\boldsymbol{h} \boldsymbol{r}^H)^{-1},现有一观测磁场\boldsymbol{e},即其预测的系统响应为\boldsymbol{Zh},它与实际观测电场的残差\boldsymbol{v} = \boldsymbol{e} - \boldsymbol{Zh}一定程度上可衡量传输函数最小二乘解的可靠性(仅仅是“一定程度”)。从而阻抗张量各元素对残差向量的贡献(定义为各元素的误差)满足:
\hat{\boldsymbol{Z}} = \boldsymbol{v} \boldsymbol{r}^H (\boldsymbol{h} \boldsymbol{r}^H)^{-1}
当参考道为\boldsymbol{r},且参与叠加的时窗个数为M,阻抗张量的总误差水平为:
\left\{
\begin{array}{**lr**}
\hat{z}_{xx} =
\frac { \overline{ V_x R_x^* }
\overline{ H_y R_y^* }
- \overline{ V_x R_y^* }
\overline{ H_y R_x^* } }
{ \overline{ H_x R_x^* }
\overline{ H_y R_y^* }
- \overline{ H_x R_y^* }
\overline{ H_y R_x^* } } &\\
\hat{z}_{xy} =
\frac { \overline{ V_x R_y^* }
\overline{ H_x R_x^* }
- \overline{ V_x R_x^* }
\overline{ H_x R_y^* } }
{ \overline{ H_x R_x^* }
\overline{ H_y R_y^* }
- \overline{ H_x R_y^* }
\overline{ H_y R_x^* } } &\\
\hat{z}_{yx} =
\frac { \overline{ V_y R_x^* }
\overline{ H_y R_y^* }
- \overline{ V_y R_y^* }
\overline{ H_y R_x^* } }
{ \overline{ H_x R_x^* }
\overline{ H_y R_y^* }
- \overline{ H_x R_y^* }
\overline{ H_y R_x^* } } &\\
\hat{z}_{yy} =
\frac { \overline{ V_y R_y^* }
\overline{ H_x R_x^* }
- \overline{ V_y R_x^* }
\overline{ H_x R_y^* } }
{ \overline{ H_x R_x^* }
\overline{ H_y R_y^* }
- \overline{ H_x R_y^* }
\overline{ H_y R_x^* } }
\end{array}
\right.
叠后阻抗张量的方差可定义为:
Var(\boldsymbol{Z}) =
{\begin{bmatrix}
{ |\hat{z}_{xx}|^2 } / M & { |\hat{z}_{xy}|^2 / M} \\
{ |\hat{z}_{yx}|^2 } / M & { |\hat{z}_{yy}|^2 / M}
\end{bmatrix}}
以上即为参考道为\boldsymbol{r}时叠后阻抗张量最小二乘解的误差估计(J Clark, T D Gamble, et. al., 1983)。必须指出的是,MT阻抗张量的“误差”并非反映各样本对期望的偏离,
而是根据系统传输函数最小二乘解(\boldsymbol{Z})和观测磁场(\boldsymbol{h})的预测电场和观测电场(\boldsymbol{e})的偏离。很多学者把MT误差和直流电法,CSAMT等的误差等同,这是完全错误的。
4.近参考和远参考
参考道一般有四种选法“Local E”、“Local H”、“Remote E”和“Remote H”,一般翻译为“近电参”、“近磁参”、“远电参”和“远磁参”。通常由于电场横向变化剧烈,从稳定性考虑多用磁场作为参考道。
考虑“Local H”与“Remote H”两种情况(分别对应向量\boldsymbol{h}和\boldsymbol{r}),实际观测的电磁场频谱均存在噪音,可表示为(噪音和信号都是未知数):
\left\{
\begin{array}{**lr**}
\boldsymbol{e} = \boldsymbol{e}_{true} + \boldsymbol{e}_{noise} &\\
\boldsymbol{h} = \boldsymbol{h}_{true} + \boldsymbol{h}_{noise} &\\
\boldsymbol{r} = \boldsymbol{r}_{true} + \boldsymbol{r}_{noise}
\end{array}
\right.
张量阻抗的最小二乘解如下:
\left\{
\begin{array}{**lr**}
\boldsymbol{Z}_{LH} = (\boldsymbol{e}_{true} + \boldsymbol{e}_{noise})
(\boldsymbol{h}_{true}^H + \boldsymbol{h}_{noise}^H)
[(\boldsymbol{h}_{true} + \boldsymbol{h}_{noise})
(\boldsymbol{h}_{true}^H + \boldsymbol{h}_{noise}^H) ] ^{-1} &\\
\boldsymbol{Z}_{RH} = (\boldsymbol{e}_{true} + \boldsymbol{e}_{noise})
(\boldsymbol{r}_{true}^H + \boldsymbol{r}_{noise}^H)
[(\boldsymbol{h}_{true} + \boldsymbol{h}_{noise})
(\boldsymbol{r}_{true}^H + \boldsymbol{r}_{noise}^H) ] ^{-1}
\end{array}
\right.
当两个信号的噪音不相干(not coherent)时,互相关操作会突出信号,压制噪音。
对于\boldsymbol{Z}_{LH},若假定MT噪音是随机的,且电磁之间不相干,
则(\boldsymbol{e}_{true} + \boldsymbol{e}_{noise}) (\boldsymbol{h}_{true}^H + \boldsymbol{h}_{noise}^H)中的噪音成分会被压制。而(\boldsymbol{h}_{true} + \boldsymbol{h}_{noise}) (\boldsymbol{h}_{true}^H + \boldsymbol{h}_{noise}^H)并无噪音压制效果,但其中的随机噪音成分可通过大量的叠加压制。
若在观测点附近有一强人工噪音源,造成\boldsymbol{e}_{noise}和\boldsymbol{h}_{noise}有强相干性,则当前时段的\boldsymbol{Z}_{LH}会严重失真,必须在叠加前手工剔除。
再极端一点,该噪音源在整个观测时段内都存在(time independent),则无论如何\boldsymbol{Z}_{LH}一定偏离真实MT传输函数甚远。
小贴士:若噪音强相干,近参的方差反而会很小,因为总观测场\boldsymbol{e}和\boldsymbol{h}是强相干的,最小二乘解公式认为里面“不含噪音”,使得残差向量\boldsymbol{v} = \boldsymbol{e} - \boldsymbol{Zh}也很小,所以这里必须再次指出,MT的方差并不表示数据噪音。
如果选择了一对“远离”测区的观测场作为参考道,可认为测区的噪音成分和参考道的噪音成分相干度很小,从而 \boldsymbol{Z}_{RH}的每一项互相关功率谱中信号成分均被放大,噪音成分均被压制。这样就有可能在强相干噪音环境下仍得到接近真实传输函数的最小二乘解。
小贴士:若噪音强相干,且能被远参考有效压制,此时阻抗张量的方差反而会变大,因为衡量方差的残差向量是\boldsymbol{e} - \boldsymbol{Z}_{RH} \boldsymbol{h},
而非\boldsymbol{e}_{true} - \boldsymbol{Z}_{RH} \boldsymbol{h}。噪音压制得越好,根据功率谱计算的方差反而会越大。
根据远参考的原理,可以得出远参考点的选择原则——“远参点处的电磁场噪音需和测区噪音不相干”。
若某点到测区的距离为当前频率趋肤深度的n倍,则测区的噪音信号在远参考点应衰减了e^{-n}。
一般来说,若远参考点选择在测区按最低频计算的7倍趋肤深度(约衰减为0.1%)以外的地方,基本可认为达到噪音弱相干的要求。但实际工作中很难确定测区背景电阻率,趋肤深度的估计往往有较大偏差(尤其在高阻区)。因此,此倍数可能要更大一些(如10倍)。
小贴士:若带远参考处理后发现高频有改善,低频和近参一样毫无改善,则表示此时参考点对于低频段来说仍“太近”。
总而言之,由于MT的张量阻抗是直接用频谱来定义估计的(信号和噪音都是未知数)。故传统意义上的加窗频率域滤波、时间域光滑、时序形态修正等可能改变电磁场功率谱比例关系的操作要非常慎重(或者说这种行为是违背MT理论基础的),有可能得到很不可靠的张量阻抗解。
经典理论框架下,有四类噪音可被有效压制:随机噪音、电磁相干度小的噪音、电磁相干度较大但仅出现在一个时段的噪音、全时段电磁强相干度但与远参考道不相干的噪音。
其压制方式分别为:足够的叠加,阻抗最小二乘解中的互相关操作及robust选谱,手工选谱,远参考处理。目前,在理论尚未有重大突破之前,其他去噪方法的理论依据都太弱且可靠性较低。
