简单的一维有限元

地球物理正问题大多需要求偏微分方程数值解，其中有限单元（FE）是非常重要的一类方法。取微分算子$L$、未知量$u$和激励函数$f$构成的一般微分方程$Lu=f$，当$u$在求解域$\Omega$的边界上满足的条件（Boundary Conditions）确定时，求$u$的问题也被称为求解边值问题（Boundary Value Problem）。
作为一篇不正经的科普，本文通篇只考虑简单的情况，比如$L$为一维空间二阶微分算子，$Lu=f$的边值问题为下式：

$$\left\{ \begin{array}{**lr**} \frac{\partial^{2} u }{ \partial x^{2}} = x + 1 &\\ x \in \Omega = [0, 1] &\\ \left. u \right|_{x=0} = 0, \left. u \right|_{x=1} = 1 & \end{array} \right.$$

当然此问题存在精确解$u(x) = {\frac{1}{6}} x^3 + {\frac{1}{2}} x^2 + {\frac{1}{3}}x$。不过我们需假定不知道它们，现在的问题是如何逼近$u(x)$。

1. 伽辽金(Galerkin)加权余量方法(Weighted Residual Method)

假定对于某个$\tilde{u}$，其残差$r$（也称余量）定义为$r=L\tilde{u}-f \neq 0$。
若某个逼近解$\tilde{u}$与真实解$u$满足$u(x)=\tilde{u}(x),\forall x \in \Omega$（即求解域中逼近解和真实解处处相等），则称$\tilde{u}$是方程$Lu=f$的一个“强解”，当然它必然满足$r(x)=0,\forall x \in \Omega$。
遗憾的是，如果函数$\tilde{u}$太复杂，我们根本无法完备的验证这一点，更何况求解它？因此，退而求其次，若函数$\tilde{u}$可用一系列简单的基函数展开，当残差与某个测试函数（也称权函数）的卷积都最小时，我们可以接受$\tilde{u}$是原问题的一个“弱解”。俗话说：“弱者也有生存的权力，强者生，弱者死的哲学在下绝不认同（by绯村剑心）”。
引入一组基函数$b_1, b_2, ..., b_n$把$\tilde{u}$展开为$c_1 b_1+ c_2 b_2+ \cdots +c_n b_n$，根据弱解条件，取一系列测试函数$w_i$和残差卷积，这些积分必须满足：

$$R_i = \int \nolimits_{\Omega} w_i r d {\Omega} = \int \nolimits_{\Omega} w_i (L\tilde{u}-f) d {\Omega} = 0$$

其中测试函数$w_i$有很多取法（如狄拉克、二范数、....），Galerkin法取$w_i$为基函数$b_i$本身，即：

$$R_i = \int \nolimits_{\Omega} b_i [ L ( c_1 b_1 + c_2 b_2 + \cdots + c_n b_n )-f] d {\Omega}$$

考虑我们的简单一维二阶微分方程$\frac{\partial^{2} u }{ \partial x^{2}} = x + 1$，假设冥冥之中有一个声音告诉你：“以耶和华、安拉和释迦牟尼的名义，逼近解必须用三次多项式展开”。即：

$$\tilde{u}(x) = c_0 + c_1 x + c_2 x^2 + c_3 x^3$$

当然，我们只能尊从三大神的统一意见，得到四个基函数$[0, x, x^2, x^3]$和四个系数$[c_0, c_1, c_2, c_3]$。四个系数怎么解出来呢？很明显，把边界条件$\tilde{u}(0)=0$和$\tilde{u}(1)=1$代入展开式可以得到：

$$\left\{ \begin{array}{**lr**} c_0 = 0 &\\ c_1 + c_2 + c_3 = 1 \end{array} \right.$$

剩下的部分则需要求Galerkin弱解条件方程，首先把二阶导求出来：

$$\frac{\partial^{2} \tilde{u}}{\partial x^{2}} = 6 c_3 x + 2 c_2$$

测试函数$w_i$分别取为$[0, x, x^2, x^3]$。$R_0=0$无需计算，$R_1$的计算过程如下：

$$\begin{align} R_1 &= \int \nolimits_{0}^{1} x (6 c_3 x + 2 c_2 - x - 1) dx \\ &= \int \nolimits_{0}^{1} [(6 c_3 - 1) x^2 + (2 c_2 - 1) x] dx\\ &= \left. {\frac{6 c_3 - 1}{3} x^3 } \right|_0^1 - \left. {\frac{2 c_2 - 1}{2} x^2 } \right|_0^1\\ &= 2 c_3 + c_2 - \frac{5}{6} \end{align}$$

再计算$R_2$，如下：

$$\begin{align} R_2 &= \int \nolimits_{0}^{1} x^2 (6 c_3 x + 2 c_2 - x - 1) dx \\ &= \int \nolimits_{0}^{1} [(6 c_3 - 1) x^3 + (2 c_2 - 1) x^2 ] dx\\ &= \left. {\frac{6 c_3 - 1}{4} x^4 } \right|_0^1 - \left. {\frac{2 c_2 - 1}{3} x^3 } \right|_0^1\\ &= \frac{3}{2} c_3 + \frac{2}{3}c_2 - \frac{7}{12} \end{align}$$

然后把所有和系数$c_i$有关的式子放到一起，得到以下线性方程组：

$$\left\{ \begin{array}{**lr**} c_0 = 0 &\\ c_1 + c_2 + c_3 = 1 &\\ c_2 + 2 c_3 = \frac{5}{6} &\\ \frac{2}{3}c_2 + \frac{3}{2} c_3 = \frac{7}{12} \end{array} \right.$$

解得$[c_0, c_1, c_2, c_3]=[0, 1/3, 1/2, 1/6]$，即：

$$\tilde{u}(x) = {\frac{1}{6}} x^3 + {\frac{1}{2}} x^2 + {\frac{1}{3}}x$$

总之，如果神仙能告诉你对$\tilde{u}$最好的基函数展开方式（给你一组完备基），使用加权余量法构建线性方程并解出系数后，我们神奇的发现，弱解$\tilde{u}(x)$刚好也是微分方程的精确解。
但要是这帮混蛋神仙故意玩你，告诉你用恶劣、邪恶的基函数去展开逼近解会如何？或者说，假使你和我一样是一个强无神论者，明显不可能与神灵亲密沟通从而得到启示，那怎么办？
的的确确，对凡人来说精确解的要求太高了。退而求其次，能否用一组足够简单的基函数来逼近近似解呢？
还有一个问题，如果我的基函数取得足够的简单（比如线性），当$u$本身非常非常复杂时，可否分段的用一组折线去逼近呢？
于是，凡人们开始不安分的想：把求解域$\Omega$分成很多子域，每个子域里用非常简单的基函数展开$\tilde{u}$，因为基函数简单，所以积分也简单，嗯，看起来可行哦......

2. 有限元法（Finite Element）

好吧，不妨就像下图这样把$x$轴的$[0,1]$区间分成$N$个子域，这里我们取$N=3$，当然你可以取成千上万。

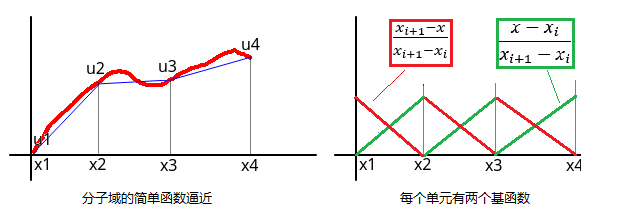
图1 有限单元的分段线性基函数展开示意图

在每个子域中，函数$u$（红色）都被逼近为分段线性函数$\tilde{u}$（蓝色）。它们可以用统一的线性基函数展开如下：

$$\left\{ \begin{array}{**lr**} \tilde{u}_i(x) = u_i \frac{x_{i+1} - x} {x_{i+1} - x_i} + u_{i+1} \frac{x - x_i} {x_{i+1} - x_i}&\\ x \in \Omega_i = [x_i, x_{i+1}] \qquad i = 1, 2, \cdots, N \end{array} \right.$$

很明显，对于每个求解子域（也叫单元，现在你明白了为啥叫有限元咯），存在两个基函数$\frac{x_{i+1} - x} {x_{i+1} - x_i}$和$\frac{x - x_i} {x_{i+1} - x_i}$（见图1右边）。第$i$个单元的基函数对应的系数分别为$u_i$和$u_{i+1}$。

注意：基函数实际上是定义在整个求解域$\Omega$上的，它们在单元内有值，而在单元外为0。

2.1 内部单元分析

我们先尝试考虑第$i$个单元，由于每个基函数都只在其所在单元内取非0值，故Galerkin加权余量积分等价于$w_i$与残差在子域$\Omega_i$中的卷积，即：

$$\begin{align} R_i &= \int \nolimits_{\Omega} w_i (L\tilde{u}-f) d {\Omega} \\ &= \int \nolimits_{\Omega_i} w_i [ \frac{\partial^{2} \tilde{u}_i(x) }{ \partial x^{2}} - (x+1)] d {\Omega_i} \end{align}$$

如图1所示，所有基函数部是线性函数，其二阶导数为0。即：

$$R_i = - \int \nolimits_{\Omega_i} w_i (x+1) d {\Omega_i} = - \int \nolimits_{x_i}^{x_{i+1}} w_i (x+1) dx$$

事情大条了，这么一搞$R_i$的表达式里没有系数$u_i$，根本得不到和系数$u_i$有关的线性方程。咋办？

注意：弱解条件的加权余量积分的表达式中必须包含待解的基函数系数。

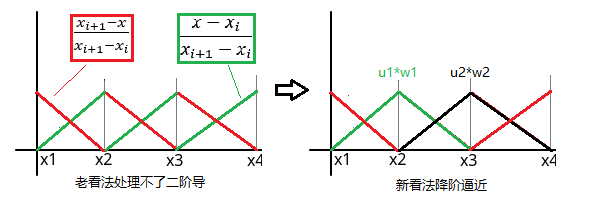
图2 根据系数所在位置去看待基函数

所以必须换个思路（见图2）来解决问题，看看系数$u_i$，它在子域$[x_{i-1}, x_i]$和$[x_i, x_{i+1}]$中都被用到。我们定义一个新子域$[x_{i-1}, x_{i+1}]$，它内部只有一个三角形的基函数不为0（见图2右的绿色和黑色三角），考虑以下Galerkin积分：

$$R_i = \int \nolimits_{x_{i-1}}^{x_{i+1}} w_i (\frac{\partial^{2} \tilde{u}(x) }{ \partial x^{2}} - x - 1) dx$$

新子域$[x_{i-1}, x_{i+1}]$上唯一具有非0值的三角形基函数的精确表达式如下：

$$w_i = \left\{ \begin{array}{**lr**} \frac{x - x_{i-1}} {x_i - x_{i-1}} \qquad x \in [x_{i-1}, x_i]&\\ \frac{x_{i+1} - x} {x_{i+1} - x_i} \qquad x \in [x_i, x_{i+1}] &\\ 0 \qquad\qquad x \notin [x_{i-1}, x_{i+1}] \end{array} \right.$$

现在二阶导项肯定不为0，但却求不出来。不过还好我们可以利用分部积分公式把它降阶，得到：

$$R_i = \left. w_i \frac{\partial \tilde{u}(x) }{ \partial x} \right|_{x_{i-1}}^{x_{i+1}} - \int \nolimits_{x_{i-1}}^{x_{i+1}} \frac{\partial w_i }{ \partial x} \frac{\partial \tilde{u}(x) }{ \partial x} dx - \int \nolimits_{x_{i-1}}^{x_{i+1}} w_i (x+1) dx$$

由于测试函数$w_i$（是基函数本身）在$x_{i-1}$和$x_{i+1}$上均为0，故上式的第一项为0。引入加权余量积分为0的弱解条件，得到以下方程：

$$\int \nolimits_{x_{i-1}}^{x_{i+1}} \frac{\partial w_i }{ \partial x} \frac{\partial \tilde{u}(x) }{ \partial x} dx + \int \nolimits_{x_{i-1}}^{x_{i+1}} w_i (x+1) dx = 0$$

先求出第一个积分项：

$$\begin{align} \int \nolimits_{x_{i-1}}^{x_{i+1}} \frac{\partial w_i }{ \partial x} \frac{\partial \tilde{u}(x) }{ \partial x} dx &= \int \nolimits_{x_{i-1}}^{x_i} \frac{\partial w_i }{ \partial x} \frac{\partial \tilde{u}(x) }{ \partial x} dx + \int \nolimits_{x_i}^{x_{i+1}} \frac{\partial w_i }{ \partial x} \frac{\partial \tilde{u}(x) }{ \partial x} dx \\ &= \int \nolimits_{x_{i-1}}^{x_i} \frac{ u_i - u_{i-1} } {(x_i - x_{i-1})^2 } dx - \int \nolimits_{x_i}^{x_{i+1}} \frac{ u_{i+1} - u_i } {(x_{i+1} - x_i)^2 } dx \\ &= \left. \frac{ u_i - u_{i-1} } {(x_i - x_{i-1})^2 } x \right|_{x_{i-1}}^{x_i} - \left. \frac{ u_{i+1} - u_i } {(x_{i+1} - x_i)^2 } x \right|_{x_{i}}^{x_{i+1}} \\ &= \frac{ u_i - u_{i-1} } {x_i - x_{i-1} } - \frac{ u_{i+1} - u_i } {x_{i+1} - x_i } \end{align}$$

类似的，再解出第二个积分项：

$$\begin{align} \int \nolimits_{x_{i-1}}^{x_{i+1}} w_i (x+1) dx &= \int \nolimits_{x_{i-1}}^{x_i} \frac{(x+1)(x-x_{i-1}) }{ x_i - x_{i-1} } dx + \int \nolimits_{x_i}^{x_{i+1}} \frac{(x+1)(x_{i+1}-x) }{ x_{i+1} - x_i } dx \\ &= \left. \frac{ \frac{x^3}{3} + \frac{(1-x_{i-1})x^2}{2} - x_{i-1}x } {x_i - x_{i-1}} \right|_{x_{i-1}}^{x_i} - \left. \frac{ \frac{x^3}{3} + \frac{(1-x_{i+1})x^2}{2} - x_{i+1}x } {x_{i+1} - x_i} \right|_{x_i}^{x_{i+1}}\\ &= \frac{(x_i-x_{i-1})(2x_i + x_{i-1} +3)}{6} + \frac{(x_{i+1}-x_i)(2x_i + x_{i+1} +3)}{6} \\ &= \frac{ (x_{i+1}-x_{i-1})(x_{i+1} + x_{i-1} + x_i + 3) } {6} \end{align}$$

现在我们可以写出关于$u_i$的方程了，如果把所有这一系列方程排列成线性方程组，它对应第$i$行，其表达式为：

$$a_{i-1} u_{i-1} + a_i u_i + a_{i+1} u_{i+1}= b_i$$

其中，三个非0系数及右端项的表达式如下：

$$\left\{ \begin{array}{**lr**} a_{i-1} = \frac{-1} {x_i - x_{i-1}} &\\ a_i = \frac{1} {x_i - x_{i-1}} + \frac{1} {x_{i+1} - x_i} &\\ a_{i+1} = \frac{-1} {x_{i+1} - x_i} &\\ b_i = - \frac{(x_{i+1}-x_{i-1})(x_{i+1} + x_{i-1} + x_i + 3)} {6} \end{array} \right.$$

2.2 边界条件处理

这里的边界条件处理方式非常简单粗暴，只需要把第一类边界条件（也叫dirichlet边界条件）$u|_{x=0}=0$，$u|_{x=1}=1$乘以系数移到方程右边即可。
以图1和图2为例，整个求解域被分成了三个单元。很显然$u_1 = 0$，$u_4 = 1$，待解向量为$[u_2, u_3]^T$。首先考虑左边界条件，方程为：

$$a_2 u_2 + a_3 u_3 = b_1 - a_1 u_1$$

代入各系数，得到：

$$(\frac{1} {x_2 - x_1} + \frac{1} {x_3 - x_2}) u_2 + \frac{-1} {x_3 - x_2} u_3 = - \frac{(x_3-x_1)(x_3 + x_2 + x_1 + 3)} {6}$$

再考虑右边界有关的方程$a_2 u_2 + a_3 u_3 = b_1 - a_4 u_4$，得到：

$$\frac{-1} {x_3 - x_2} u_2 + (\frac{1} {x_3 - x_2} + \frac{1} {x_4 - x_3}) u_3 = - \frac{(x_4-x_2)(x_4 + x_3 + x_2 + 3)} {6} + \frac{1}{x_4 - x_3}$$

不妨设所有单元是等距分割的（$x_4-x_3 = x_3-x_2=x_2-x_1=\frac{1}{3}$），此时线性方程组为：

$$\left\{ \begin{array}{**lr**} 6 u_2 - 3 u_3 = - 4/9 &\\ -3 u_2 + 6 u_3 = 22/9 \end{array} \right.$$

求解得到$u_2=\frac{14}{81}$， $u_3=\frac{40}{81}$。很振奋人心的是这两个值和$u(x) = {\frac{1}{6}} x^3 + {\frac{1}{2}} x^2 + {\frac{1}{3}}x$的验算结果完全一致。
但不要高兴得太早：首先，这只是运气好，并非所有问题都会满足节点上存在精确近似；其次，即使我们运气这么好，除了四个系数所在点，其它点和精确解相比都有很大误差（见图3）。只需要细看图1就知道误差产生的原因。
当然，驴子都想得到，只要剖分了足够多的单元，整体逼近精确解的精度会更高。图3绘制了剖分为3和10个单元的情况，看起来10个单元的效果不错哦。

小贴士：这里我们用了等距剖分，但是没人要求你一定要这样搞，非均匀剖分其实更占主流。

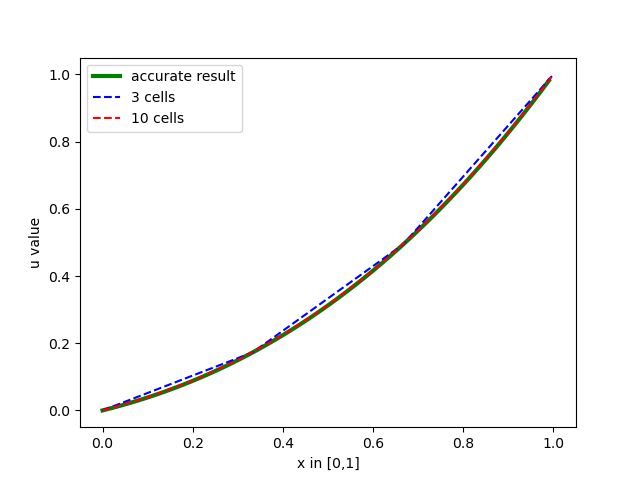
图3 精确解和有限元数值解的对比

3. 总结

这只是一个小小的科普文，举的例子也超级简单，但凡事总要从简到繁，一口吃不了个胖子。
现代有限元方法已发展得非常成熟，选定单元剖分和基函数后，其加权余量积分、矩阵组装、线性系统的解法等工作基本可以按图索骥。
可能有些人会觉得有限元的精度高于有限差分，因为“有限差分只能获取采样点处的函数值（对应$u_i$）”。我不知道是哪位神仙这么武断，但请考虑一下：非采样点处的函数值在有限差分中是用线性插值得到的，而在有限元中是用基函数展开式直接求取的。问题来了，一阶有限差分和一阶有限单元在非采样点处的精度哪个高？都是线性的，你有限元得瑟啥？
实际上同阶的有限单元和有限差分相比，其优势在于对求解区域的剖分方式更灵活，而不是其数值解精度。

小贴士：有限元方法中最重要的部分在于基函数选取，在Galerkin加权余量积分中，测试函数（或权函数）直接选取为基函数本身，继而构建弱解条件得到系数的线性方程组。任何一篇讲有限元的文献都随处可见“基函数”三个大字。所以说，搞有限元就是在搞那个啥。鉴于搞那个啥是一种目前还没有被主流社会认可的行为，因此有些那个啥佬们羞羞答答的不说基函数，而取了个名字叫“形函数”。小样，欲盖弥彰（手动狗头）。