复杂的一维有限元

《简单的一维有限元》已经介绍了如何用Galerkin有限元法求解以下一维边值问题：

$$\left\{ \begin{array}{**lr**} \frac{\partial^{2} u }{ \partial x^{2}} = x + 1 &\\ x \in \Omega = [0, 1] &\\ \left. u \right|_{x=0} = 0, \left. u \right|_{x=1} = 1 & \end{array} \right.$$

但仍有些基础问题值得讨论。鉴于搞有限元就是在搞(和谐)基，所以为了搞出新花样，搞出新特色，对基函数、加权余量积分的更进一步理解是非常必要。

1. Galerkin加权余量法的不正经理解

逼近函数$\tilde{u}$的Galerkin弱解条件为残差$r$满足下式：

$$R_i = \int \nolimits_{\Omega} w_i r d {\Omega} = \int \nolimits_{\Omega} w_i (L\tilde{u}-f) d {\Omega} = 0$$

它看起来非常神秘，极度晦涩，甚至有点莫名其妙。为啥残差满足这个东西就OK了？测试函数$w_i$取成各基函数是何道理？为积分计算方便取成$w_i=1$不行吗？
其实这个问题可以用某种不正经的几何事实来解释：在泛函分析中$w_i$即是一个函数，也可以理解为一个向量，$\int \nolimits_{\Omega} w_i r d {\Omega}$实际上就是向量$w_i$和残差向量$r$的内积，记为$\left< w_i, r \right>_\Omega$。内积和向量夹角有关，满足Galerkin弱解条件时，要么即残差为0，要么它与每个基函数都互相垂直。
所有逼近函数$\tilde{u}$组成的空间可视为由所有基函数张成的一个平面（图1左）。Galerkin条件取残差$r$垂直此平面的情况，用不严谨的几何来理解：如果从平面外一点走入平面，沿垂直方向路径最短。当然，若$r$刚好取到0值，则弱解条件和强解条件一致。

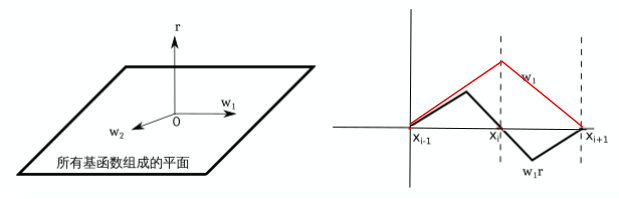
图1 Galerkin加权余量积分，左：残差向量垂直基函数平面；右：一维加权残差函数

另外，一维一阶有限元的基函数在每个子域$[x^{i-1}, x^{x+1}]$内为三角函数（图1右的红线）。观察函数的图像，Galerkin弱解条件有两层意思：一方面，只要积分为0，该单元的逼近函数在全局求解域下满足弱解条件；另一方面，视积分为无穷求和，内积为0也可不严谨的理解为子域内残差函数的加权平均值（权值为基函数）为0。

小贴士：Glerkin法只是加权余量法的一种，测试函数（权函数）还可以按子域取为1（子域法）；或在配置好的点上取狄拉克函数$\delta$（配点法）；或取为残差函数本身（最小二乘法）；还可取为求解域的空间基向量（矩法）等等。

2. 是否必须使用分部积分法

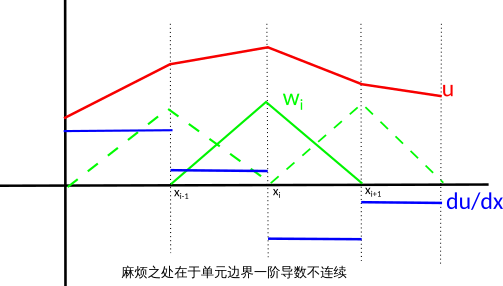
图2 分段逼近函数、基函数及其一阶导数

由于逼近函数$\tilde{u}$在每个单元内的一阶导在$x_i$处不连续（图2）。所以为了解决子域$[x^{i-1}, x^{x+1}]$中的二阶不可导引起的问题，需使用分部积分法得到：

$$R_i = \left. w_i \frac{\partial \tilde{u}(x) }{ \partial x} \right|_{x_{i-1}}^{x_{i+1}} - \int \nolimits_{x_{i-1}}^{x_{i+1}} \frac{\partial w_i }{ \partial x} \frac{\partial \tilde{u}(x) }{ \partial x} dx - \int \nolimits_{x_{i-1}}^{x_{i+1}} w_i (x+1) dx$$

这会给我们一个错觉，认为构建二阶微分方程的线性基函数弱解依赖分部积分方法。但如果引入一个特殊函数，此错觉便不攻自破。这个神奇的函数就是狄拉克（Dirac）函数$\delta$，其定义为：

$$\left\{ \begin{array}{**lr**} \delta(x)=0 \qquad when \quad x \neq 0 &\\ \int \nolimits_{-\infty}^{-\infty} \delta (x) dx = 1 \end{array} \right.$$

在物理上Dirac函数可以用来表示作用在点$x_0$上的一个单位脉冲，记为$\delta (x-x_0)$。它在奇点$x_0$处为$\infty$，此外处处为0。Dirac函数还有很多有趣的性质，比如：
1. 取$\forall$子域$D$，且$x_0 \in D$，$\int \nolimits_{D} \delta (x-x_0) dx = 1$。
2. 取$\forall$子域$D$，且$x_0 \in D$，对于$\forall f(x)$，$\int \nolimits_{D} f(x) \delta (x-x_0) dx = f(x_0)$。
3. 若函数$f(x)$在点$x_0$处不连续，且当$x<x_0$时$f(x)=a$，$x>x_0$时$f(x)=b$，则该函数的一阶导数为$f'(x)=(b - a) \delta (x-x_0)$。
第3条性质让人相当郁闷，明明在$x_0$点上是没有导数的，哪里又冒出来这么个式子。不过呢，只要一想Dirac函数是物理学家搞出来的我马上就释怀了，又是物理学家，还要搞(和谐)基，还有什么搞不出来的呢？
考虑阶梯函数：

$$\theta(x)= \left\{ \begin{array}{**lr**} 0 \qquad x<0 &\\ 1 \qquad x>0 \end{array} \right.$$

已经证明$\theta ' (x) = \delta(x)$，将$\theta(x)$进行平移、拉伸，可定义$f(x)= (b-a)\theta(x-x_0) + a$，故$f'(x)=(b-a)\delta(x-x_0)$。这真是一个毁三观的结论，不过有兴趣可以在google上搜索一下，阶梯函数的导数为Dirac函数的证明过程也是一通骚操作。

现在可以求二阶导了，观察图2，直接利用Dirac函数的第3条性质得到：

$$\frac{\partial^{2} \tilde{u}(x)}{\partial x^{2}} = \sum_{i=1}^N \frac{\partial \tilde{u}_i'(x)}{\partial x} = \sum_{i=1}^N (b_i - a_{i}) \delta (x - x_i)$$

其中，下标$i$表示单元编号，$b_i=\frac{u_{i+1} - u_i}{x_{i+1}-x_{i}}$， $a_i=\frac{u_{i} - u_{i-1}}{x_{i}-x_{i-1}}$。直接对此表达式应用Galerkin积分，对于每个基函数$w_i$，有：

$$\int \nolimits_0^1 [\sum_{j=1}^N (b_j - a_{j}) \delta (x - x_j)] w_i(x) dx - \int \nolimits_0^1 w_i(x)(x+1) dx = 0$$

注意，上式括号内的下标$j$和$w_i$的下标$i$的意义不同，前者表示二阶导全局展开的基函数编号，后者是当前Galerkin积分的测试函数编号。根据Diract函数的第2条性质把第一个积分消除，得到：

$$\sum_{j=1}^N (b_j - a_{j}) w_i(x_j) - \int \nolimits_0^1 w_i(x)(x+1) dx = 0$$

观察图2可以得出：当$i \neq j$时，$w_i(x_j)=0$,当$i=j$时，$w_i(x_j)=1$,上式进一步简化为：

$$(b_i - a_{i}) - \int \nolimits_0^1 w_i(x)(x+1) dx = 0$$

把$b_i$和$a_i$的表达式代入即可算出与分部积分法完全一致的方程:

$$\frac{u_{i+1}-u_i}{x_{i+1}-x_{i}} - \frac{u_{i}-u_{i-1}}{x_{i}-x_{i-1}} - \int \nolimits_0^1 w_i(x)(x+1) dx = 0$$

小贴士： 现在我们知道，线性基函数求二阶导问题时，分部积分法并不是构建弱解的关键。弱解成立的基本因素是Galerkin加权余量积分本身。Dirac函数并不满足微积分的传统定义，经常有一些反直觉的诡异行为，所以实际工程应用中老老实实的分部积分为妙，勿为言之不预也。

3. 有限元矩阵装配

实际工程应用中，Galerkin积分通常可以写为线性算子，组成刚度矩阵（stiffness matrix）（简称“组刚”）和右端项。考虑之前分部积分得到的Galerkin弱解条件：

$$\int \nolimits_{x_{i-1}}^{x_{i+1}} \frac{\partial w_i }{ \partial x} \frac{\partial \tilde{u}(x) }{ \partial x} dx - \int \nolimits_{x_{i-1}}^{x_{i+1}} w_i (x+1) dx = 0$$

刚度矩阵$\boldsymbol{K}$满足：

$$\boldsymbol{K} \boldsymbol{u} = \boldsymbol{b}$$

其中，$\boldsymbol{u}=[u_2, u_3, \cdots, u_{N}]$，（边界上$u_1$和$u_{N+1}$满足dirichlet边界条件，已知）；右端项$\boldsymbol{b}$和第二项积分及边界条件有关。

小贴士： 有些力学问题中，右端项也可以写为$\boldsymbol{b} = \boldsymbol{c} + \boldsymbol{M}\boldsymbol{s}$的形式，其中$\boldsymbol{c}$为只与边界条件有关的稀疏向量，$\boldsymbol{s}$为原微分系统$Lu=s$的“源项”。此时$\boldsymbol{M}$也被称为质量矩阵（mass matrix）。

3.1 等参单元

之前构建积分的线性算子时有一堆${x_i}$需要考虑，极易写错下标。所以我们把网格单元投影到同一标准单元（图3）上处理。

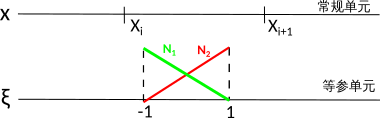
图3 等参单元及基函数

在第$i$个单元内，基函数展开为$\tilde{u}=\sum_{i=1}^n w_i(x) u_i$，投影后新插值基函数为$\tilde{u}=\sum_{i=1}^m N_i(\xi) u_i$，这里$n=m=2$，$u_1$和$u_2$分别表示单元两端的系数。
每个新单元的待解系数个数和原单元相同，叫作“等参元”，如果$n<m$叫“超参元”，反之则叫“亚参元”。
使用等参元的原因是高维、高阶插值基函数时直接积分极易出错，使用标准等参元后处理起来方便一些，但一维一阶问题的等参元并没有太大优势。针对我们的问题，等参元有以下性质：

$$\left\{ \begin{array}{**lr**} \tilde{u}^{(i)}(\xi) = N_1^{(i)} (\xi) u_i + N_2^{(i)} (\xi) u_{i+1} &\\ x^{(i)}(\xi) = N_1^{(i)} (\xi) x_i + N_2^{(i)} (\xi) x_{i+1} &\\ N_1^{(i)} (\xi) = (1- \xi) / 2 \qquad N_2^{(i)} (\xi) = (1+\xi) / 2&\\ dx^{(i)} = \frac{x_{i+1} - x_i}{2} d{\xi} \end{array} \right.$$

上式的上标$(i)$表示在第$i$个单元内。不妨设$h_i=x_{i+1} - x_i$，考虑Glerkin积分的第一项：

$$\int \nolimits_{x_{i-1}}^{x_{i+1}} \frac{\partial w_i }{ \partial x} \frac{\partial \tilde{u}(x) }{ \partial x} dx = \int \nolimits_{x_{i-1}}^{x_{i}} \frac{\partial w_i }{ \partial x} \frac{\partial \tilde{u}^{(i-1)} }{ \partial x} dx + \int \nolimits_{x_{i}}^{x_{i+1}} \frac{\partial w_i }{ \partial x} \frac{\partial \tilde{u}^{(i)} }{ \partial x} dx$$

我们可以首先麻烦的直接计算等式右边的第二个积分，看看可以得到什么：

$$\begin{align} \int \nolimits_{x_{i}}^{x_{i+1}} \frac{\partial w_i }{ \partial x} \frac{\partial \tilde{u}^{(i)} }{ \partial x} dx &= \int \nolimits_{-1}^{1} \frac{\partial w_i }{ \partial x} \frac{\partial \tilde{u}^{(i)} }{ \partial x} \frac{\partial x^{(i)} }{ \partial {\xi}} d{\xi} \\ &= \frac{h_i}{2} \int \nolimits_{-1}^{1} \frac{\partial w_i }{ \partial \xi} \frac{\partial \xi }{ \partial x} \frac{ \partial \tilde{u}^{(i)} }{ \partial \xi} \frac{\partial \xi }{ \partial x} d{\xi} \\ &= \frac{2}{h_i} \int \nolimits_{-1}^{1} \frac{\partial w_i }{ \partial \xi} \frac{ u_{i+1} - u_{i} } {2} d{\xi} \\ &= \frac{u_{i+1} - u_{i}}{h_i} \int \nolimits_{-1}^{1} - \frac{1}{h_i} \frac{\partial x}{\partial \xi} d{\xi} \\ &= \frac{u_{i+1} - u_{i}}{h_i} \int \nolimits_{-1}^{1} -\frac{1}{2} d{\xi} \\ &= \frac{u_{i} - u_{i+1}}{h_i} \end{align}$$

嗯，此时我不禁深深的皱起了眉头，绕这么多弯子干吗？直接在$x$上积分不是更快捷吗？
但是观察图3可以得到一个事实，$N_1$基函数（图3绿线）的一阶导满足以下关系：

$$\frac{\partial w_i^{(i)} }{ \partial \xi} = \frac{\partial N_1^{(i)} }{ \partial \xi} = - \frac{1}{2}$$

原积分项其实可以直接写为：

$$\int \nolimits_{x_{i}}^{x_{i+1}} \frac{\partial w_i }{ \partial x} \frac{\partial \tilde{u}^{(i)} }{ \partial x} dx = \frac{\partial \xi^{(i)}}{\partial x} \int \nolimits_{-1}^{1} \frac{\partial N_1^{(i)} }{ \partial \xi} \frac{\partial \tilde{u}^{(i)} }{ \partial \xi} d{\xi}$$

小贴士： 在高维或高阶插值基函数中，$x$对$\xi$的偏导数会变成和雅可比行列式有关的问题，积分号内部的函数会更简单通用，适合组刚。

同样，我们可以快速的写出：

$$\begin{align} \int \nolimits_{x_{i-1}}^{x_{i}} \frac{\partial w_i }{ \partial x} \frac{\partial \tilde{u}^{(i-1)} }{ \partial x} dx &= \frac{\partial \xi^{(i-1)}}{\partial x} \int \nolimits_{-1}^{1} \frac{\partial N_2^{(i-1)} }{ \partial \xi} \frac{\partial \tilde{u}^{(i-1)} }{ \partial \xi} d{\xi} \\ &= \frac{2}{h_{i-1}} \int \nolimits_{-1}^{1} \frac{1}{2} \frac{u_i - u_{i-1}}{2} d{\xi} \\ &= \frac{u_i - u_{i-1}}{h_{i-1}} \end{align}$$

3.2 单元刚度矩阵和整体组刚

我们不象之前那样考虑两个单元的三角形基函数问题，而是先对图3中第$i$个单元的两个基函数分别解出其Galerkin积分。根据上一节的推导，可以直接写出以下公式：

$$\left\{ \begin{array}{**lr**} g_{-}^{(i)}=\int \nolimits_{x_{i}}^{x_{i+1}} \frac{\partial w_1^{(i)} }{ \partial x} \frac{\partial \tilde{u}^{(i)} }{ \partial x} dx = (u_{i} - u_{i+1}) / h_i &\\ g_{+}^{(i)}=\int \nolimits_{x_{i}}^{x_{i+1}} \frac{\partial w_2^{(i)} }{ \partial x} \frac{\partial \tilde{u}^{(i)} }{ \partial x} dx = (-u_{i} + u_{i+1}) / h_i \end{array} \right.$$

其中，$w_1^{(i)}$对应等参元中的基函数$N_1$，$w_2^{(i)}$对应$N_2$。很自然的，上面的公式可用以下线性系统表示：

$$\boldsymbol g^{(i)} = \begin{bmatrix} g_{-}^{(i)} \\ g_{+}^{(i)} \end{bmatrix} = \boldsymbol K^{(i)} \boldsymbol u^{(i)} = \frac{1}{h_i} \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix} \begin{bmatrix} u_i \\ u_{i+1} \end{bmatrix}$$

当然以下关系必然是颠扑不破的真理之一：

$$\begin{bmatrix} K_{11}^{(2)} & K_{12}^{(2)} & 0 & 0 \\ K_{21}^{(2)} & K_{22}^{(2)} & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots \\ \end{bmatrix} \begin{bmatrix} \vphantom{K_{11}^{(2)}} u_2 \\ \vphantom{0} u_3 \\ \vphantom{0} \dots \\ \vphantom{\vdots} u_{N} \end{bmatrix} = \begin{bmatrix} \vphantom{K_{11}^{(2)}} g_{-}^{(i)} \\ \vphantom{0} g_{+}^{(i)} \\ \vphantom{0} 0 \\ \vphantom{\vdots} \vdots \end{bmatrix}$$

更进一步，把第2个单元和第1个单元的线性系统相加，真理加真理肯定又是一个真理：

$$\left( \begin{bmatrix} K_{11}^{(2)} & K_{12}^{(2)} & 0 & 0 \\ K_{21}^{(2)} & K_{22}^{(2)} & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots \\ \end{bmatrix} + \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & K_{11}^{(3)} & K_{12}^{(3)} & 0 \\ 0 & K_{21}^{(3)} & K_{22}^{(3)} & 0 \\ \vdots & \vdots & \vdots & \vdots \\ \end{bmatrix} \right) \begin{bmatrix} \vphantom{K_{11}^{(2)}} u_2 \\ \vphantom{0} u_3 \\ \vphantom{0} \dots \\ \vphantom{\vdots} u_{N} \end{bmatrix} = \begin{bmatrix} \vphantom{K_{11}^{(2)}} g_{-}^{(2)} \\ \vphantom{0} g_{-}^{(2)} + g_{+}^{(3)} \\ \vphantom{0} 0 \\ \vphantom{\vdots} \vdots \end{bmatrix}$$

以此类推，很自然的，刚度矩阵$\boldsymbol K$的表达式就是把上面的过程迭代一下，得到：

$$\begin{bmatrix} K_{11}^{(2)} & K_{12}^{(2)} & 0 & 0 & 0 & 0\\ K_{21}^{(2)} & K_{22}^{(2)} +K_{11}^{(3)} & K_{12}^{(3)} & 0 & 0 & 0\\ 0 & K_{21}^{(3)} & K_{22}^{(3)} + K_{11}^{(4)} & K_{12}^{(4)} & 0 & 0\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & K_{21}^{(N-2)} & K_{22}^{(N-2)} + K_{11}^{(N-1)} & & K_{12}^{(N-1)}\\ 0 & 0 & 0 & 0 & K_{21}^{(N-1)} & & K_{22}^{(N-1)} + K_{11}^{(N)}\\ \end{bmatrix}$$

如此，$\boldsymbol K \boldsymbol u = [g_{-}^{(2)}, g_{+}^{(2)} + g_{-}^{(3)}, g_{+}^{(3)} + g_{-}^{(4)}, \cdots, g_{+}^{N}]^{T}$ 。

小贴士： 在之前的简单有限元中我们每次分析矩阵的一行，这对于一维一阶有限元反而更简单明晰。但是如果是高维、高阶问题，刚度矩阵的稀疏模式（sparse parttern）会变得很复杂，此时标准化处理方式会简单许多。

3.3 右端项

和组刚一样，首先写出单元$i$上的积分$\int \nolimits_{x_{i-1}}^{x_{i+1}} w_i (x+1) dx = s_{+}^{(i-1)} + s_{-}^{(i)}$，之前我们已经求出了第$i$个单元内它们满足的表达式：

$$\left\{ \begin{array}{**lr**} s_{-}^{(i)}=\frac{h_i}{6} (2x_i + x_{i+1} + 3) &\\ s_{+}^{(i)}=\frac{h_i}{6} (x_i + 2x_{i+1} + 3) \end{array} \right.$$

与“源”相关的向量式表达为$\boldsymbol{s} = [s_{+}^{(1)} + s_{-}^{(2)}, s_{+}^{(2)} + s_{-}^{(3)}, \cdots, s_{+}^{(N-1)} + s_{-}^{(N)}]^{T}$。
与边界条件有关的向量表达式为$\boldsymbol{c} = [- K_{22}^{(1)}u_1, 0, \cdots,0, - K_{12}^{(N)}u_{N+1}]^{T}$。
右端项向量可表示为$\boldsymbol{b} = \boldsymbol{s} + \boldsymbol{c}$。

4. 总结

和简化版有限元不同的是，这篇文章重新讨论了Galerkin有限单元法里的几个细节问题。
Galerkin加权余量积分可以从几何或加权平均两个视角去理解，弱解形式的意义很明确。
我们换了一个姿势，引入Dirac函数代替分部积分降阶，并且采用了更标准的“单元分析”从局部到整体构建线性系统，这是钦定的正确搞(和谐)基方式。
我们引入了等参元，通过积分换元写出局部单元小刚度矩阵，然后整体组刚。
再次声明，并非所有问题都要标准搞(和谐)基。都2020年了，很多问题与其使用等参元的奇技淫巧，还不如直接用mathematica软件暴力积分。
我们尚没有介绍高阶有限元，但其原理和步骤基本类似：1）选基；2）展基；3）积基；4）积基线性化；5）解基系数。说了半天，步步搞(和谐)基：）。