流与惰性求值
在学习C语言的fprintf函数时,我们会接触到"文件流"的概念。比如你写了如下的代码:
FILE *fp = fopen("somefile.txt", "w");
fprintf(fp, "write something into file stream\n");
fclose(fp);
fp是一个指向FILE类型的指针(文件流指针),这种数据结构叫做“文件流”。那么有一个问题,为什么文件是"流"? 还有一个问题,
python中的for i in range(5):和for i in [1,2,3,4,5]:是否是同样的东西?实际上,range(5)也是一个流(stream)。我们尝试解释
stream这种编程范式的本质。你会发现不仅文件是流,流其实是一种编写线性代码的高级范式,高效的流实现还需要涉及“惰性求值”。
1. 流是一种通用过程¶
考虑一个计算正整数区间[a,b]内的所有素数和的过程。Scheme语言迭代风格(虽然是递归语法)的计算程序很可能是这样:
(define sum-primes-1
(lambda (a b) ;定义sum-primes-1是一个关于(a,b)的函数
(define iter ; 内部嵌套定义个iter函数
(lambda (n sum) ; 其参数是(n, sum)
(cond ; 其函数体为:
[(> n b) sum] ; 如果n>b - 返回 sum
[(prime? n) (iter (+ n 1) ; 如果n是素数 -
(+ n sum))] ; 返回iter(n+1, n+sum)
[else (iter (+ n 1) sum)]))) ; 否则 - 返回 iter(n+1, sum)
(iter a 0))) ; sum-primes-1的函数体为 iter(a, 0)
(define comp-in-a-b ;首先,定义个通用递归过程
(lambda (a b yes-or-no do-when-yes) ; 输入区间,以及判断过程,后续执行方式
....))
(define sum-biger-than-7 ;这里我不需要再手写一遍递归了
(lambda (a b)
(comp-in-a-b
(lambda (x) (> x 7)) ;注意yes-or-no是一个函数,而不是变量
(iter ..... ))))
但以上方式只能处理区间内求和这种单判断分支的递归,不能应对两个判断分支的情况。比如,对素数求和,非素数加1的算法无法用comp-in-ab函数构建。
我们还有另外一个思维方式,假如你对链表比较熟悉的话,首先不考虑计算效率,以下方案应该是可行的:区间[a,b]内的所有素数按顺序排出来会形成一个链表(list),然后对链表进行求和,而所有素数构成的链表可以通过对正整数的链表进行筛选得到,整个算法可以表示成一系列的链表遍历操作。
对于链表,大部分语言都会提供一些高阶操作,如map、filter、accumulate等,它们的实现分别如下:
(define map ; map函数,
(lambda (proc items) ; 对链表的每个元素应用过程proc
(if (null? items) ; 如果items是空表
nil ; 返回空
(cons (proc (car items) ; 否则创建新表,第一个元素为proc(item1)
(map proc (cdr items))))))) ; 然后对剩下的元素递归调用map函数
(define filter ; filter函数
(lambda (predicate items) ; 参数为判真函数pedicate, 链表本身
(cond
[(null? items) ; 如果空返回空
nil]
[(predicate (car items)) ; 如果第一个元素判断条件为真,返回新链表,
(cons (car items) ; 其首元素不变,剩余部分递归调用filter
(filter predicate (cdr items)))]
[else (filter predicate (cdr items))]))) ;否则,返回对剩余部分递归filter的结果
(define accumulate ; 累计函数accumulate
(lambda (op init items) ; 参数为操作op, 初始值init, 链表本身
(if (null? items) ; 如果链表为空,
init ; 返回初始值init
(op (car items) ; 否则,op(首元素, 其它元素的accumlate)
(accumulate op init (cdr items))))))
(define enum-ab ; 区间穷举函数enum-ab,构造自然数链表
(lambda (a b) ; 给定区间[a,b]
(if (> a b) ; 如果a>b,返回空
nil ; 否则返回新链表,首元素为a
(cons a (enum-ab (+ a 1) b))))) ; 其它元素是对[a+1,b]的enum-ab调用
(map abs (list -10 2 -11 17)) ; 返回'(10 2 11 17),对原表所有元素求绝对值
(filter odd? (list 1 2 3 4 5)) ; 返回'(1 3 5),取出链表中的奇数
(accumulate + 0 (list 1 2 3)) ; 对'(1 2 3)求和,返回6
(accumulate * 1 (list 1 2 4)) ; 对'(1 2 4)求乘积,返回8
(enum-ab 1 4) ; 输入区间为[1,4], 返回'(1 2 3 4)
(define sum-primes-2
(lambda (a b) ;这里的sum-prime-2直接调用了高阶函数
(accumulate ;用c语言的形式可以类似的写为
+ ;accumulate(+, 0, filter(prime?, enum-ab(a, b)))
0 ; 1. x = enum-ab(a, b)
(filter ; 2. y = filter(prime?, x)
prime? ; 3. accumulate(+, 0, y)
(enum-ab a b)))))
sum-primes-2的函数体变为一行(上面的代码打印成多行是为了人类可读),需要4个高阶函数,是不是有点脱裤子那啥。:)但请别着急,再看另外一个斐波拉契数列的例子,如果我们要列举区间[0,n]内所有偶斐波拉契数,暴力编写的丐版程序可能如下:
;首先写一个求斐波拉契数的程序
(define fib
(lambda (n)
(if (<= n 1)
n
(+ (fib n-1) (fib n-2)))))
;生成[0,n]内的偶fibonacci数的链表(当然你可以写得更清晰,但逻辑是一样的)
(define even-fibs-1
(lambda (n) ;even-fibs函数是对next(k)这个递归函数的调用
(define next ; next(k) 函数定义如下
(lambda (k)
(if (> k n) ; 如果k>n了,返回空表
nil
(if (even? (fib k)) ; 否则,继续判断,如果fib(k)是偶数
(cons (fib k) (next (+ k 1))) ;返回 [fib(k), next(k+1)]
(next (+ k 1)))))) ;否则返回next(k+1)
(next 0))) ;even-fibs(n)等价于递归调用next(0)
对比函数sum-primes-1和even-fibs-1的代码,它们是如此的不同。原因也貌似很自然,一个是求和,另外一个是生成链表。
但是从高阶函数map、filter和accumulate等的视角来看,两个程序的逻辑却是很类似的。譬如,偶斐波拉契数链表也可以实现成下面这样:
(define even-fibs-2
(lambda (n)
(accumulate;用c语言的形式可理解为
cons ;accumulate(cons, '(), filter(even?, map(fib, enum-ab(a, b))))
'() ; 1. x = enum-ab(0, n)
(filter ; 2. y = map(fib, x)
even? ; 3. z = filter(even?, y)
(map ; 4. accumulate(cons, '(), z)
fib
(enum-ab 0 n))))))
Ah-ha!!!看似完全不同的东西,实际上在高阶函数看来,居然有很多共性。
这个共性是什么呢?看起来好像是数据链表流过一台台机器(高阶函数),然后变成了我们需要的东西。一头头猪经过加工车间里面各道工序,变成了一串火腿肠。
图1解释了sum-primes-2和even-fibs-2这两个计算过程的共性,并展示了其它类似计算过程的高阶函数表示。
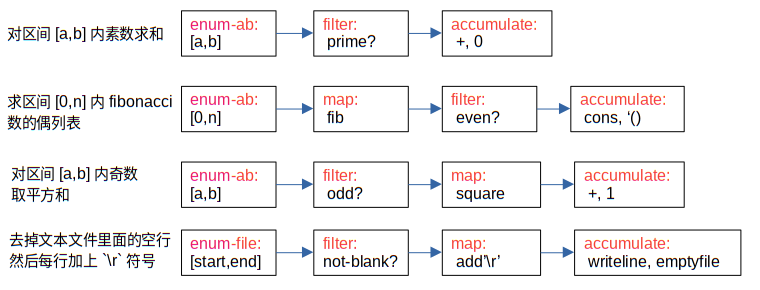
我们看到,无论是求平方和、生成数列,还是进行文件转换,在图1的视角中都是一串数据(比如链表)流经生产线的过程。这一类型的编程泛式,就是流模式,英文是stream。
小贴士:Richard Waters于1979年开发了一个分析当时的Fortran科学计算程序包的程序,发现程序包里面足足有90%的计算程序满足图1的范式。所以千万不要忽略高阶函数的威力。
流模式的好处在于提供了一种通用的方式去表达算法。先干什么,再干什么一目了然,没有各种跳转和乱入。这种代码称为线性代码,与之相对的代码也可称为“面条代码”,或者“屎山”。
但天下没有免费的午餐!到目前为止,流模式程序的执行效率极其低下,无论是空间效率还是时间效率。如果我们要对区间[1,10000000]内的奇数求平方和,流模式的编程方式起码要生成三个长链表并进行三个O(n)的遍历。这会慢得抠jio。
有没有办法解决效率问题呢?毕竟吃白食的感觉是很棒的。
2. 流的抽象与惰性求值¶
为了让问题更加一般化,我们必须定义一个通用类型stream,它有一个构造函数cons-stream,两个选择函数stream-head和stream-rest,分别对应创建一个流、取得流的第一个元素、取得剩余流。满足条件如下:
(stream-head (cons-stream x y)) = x ;由x和y组成的流的头元素是x
(stream-rest (cons-stream x y)) = y ;由x和y组成的流的剩下部分是y
链表无非是(cons 1 (cons 2 (cons 3 nil)))这样的东西——简记为(list 1 2 3)。鉴于流和链表的相似性,第1节的链表基本函数在流中应该也有类似的版本,比如取第n元素的stream-ref,通用变换的stream-map,stream-filter,stream-accumulate等等,代码如下:
(define stream-ref ;取流的第n个元素
(lambda (s n) ;如果n等于0就取 stream-head(s)
(if (= n 0) ;否则递归 stream-ref(stream-rest(s), n-1)
(stream-head s)
(stream-ref (stream-rest s) (- n 1)))))
(define stream-map ;对流的每个元素进行变换,变换函数为proc
(lambda (proc s) ; 如果s是空流,返回nil
(if (null? s) ; 1. a=proc(stream-head(s))
nil ; 2. b=stream-map(proc, stream-rest(s))
(cons-stream (proc (stream-head s)) ;3. cons-stream(a, b)
(stream-map proc (stream-rest s))))))
(define stream-enum-ab ;从区间[a,b]中生成一个流,和前面的enum-ab函数类似
(lambda (a b) ;但是她们生成的数据结构是完全不同的,请往后看
...))
(define stream-filter ;对一个流按判断条件进行筛选类似于前面的filter函数
(lambda (predicate s)
...))
stream-cons代替了cons,stream-head代替了car,stream-rest代替了cdr。所以,以下算法的表达与第一节完全类似,只是换了个马甲:a)从[100,100000]这个区间建立一个流,比如是s1;
b)取这个流的素数部分,生成一个新流s2;
c)取s2的除首个元素的剩余部分,得到s3;
d)取s3的第一个元素。
这个算法的代码如下:
(stream-head ;stream-head(s3)
(stream-rest ;s3 = stream-head(s2)
(stream-filter prime? ;s2 = stream-filter(prime?, s1)
(stream-enum-ab 100 100000))))
cons-stream函数能够赋予一种穿越能力,当最外层列举到103时,其他更大的素数不会被显式在内存中枚举生成。这种按需求值的能力还有一个称呼——延迟求值,或惰性求值。
小贴士:没错,有了惰性求值,流和链表变成了不同的东西,cons-stream和cons操作类似,但生成的数据结构完全不同。流不是链表。
为了局部的(我们不想改变语言的求值顺序)引入惰性求值,需要两个函数delay和force。(delay a)表示“许诺”a会在需要的时候才被求值,而(force (delay a))表示现在就对a进行求值。从而惰性求值版本的stream可实现如下:
(define cons-stream ;cons-stream构造一个流
(lambda (x y) ; 等价于序对(x . (delay y))
(cons x (delay y))))
(define stream-head
(lambda (s) ;stream-head返回流的头
(car s))) ;对应上面的 x
(define stream-rest
(lambda (s) ;我们要对(delay y)强制求值
(force (cdr s)))) ;得到上面的 y
enum-ab的实现,只是把cons替换成cons-stream。stream-filter函数我们也写出来,仍然几乎是照抄filter函数:
(define stream-enum-ab
(lambda (a b)
(if (> a b)
nil
(cons-stream a (stream-enum-ab (+ a 1) b)))))
;注意:这一行a我们确实给出了,但后面的(stream-enum-ab (+ a 1) b)不会被立刻求值
;因为被delay了,也就是说这个流并不是a到b之间的长链表,而是(a . y),y只是一个许诺。
(define stream-filter
(lambda (predicate s)
(cond
[(null? s) nil]
[(predicate (stream-head s))
(cons-stream (stream-head s)
(stream-filter predicate (stream-rest s)))]
;注意:这里的递归会被延迟求值
[else (stream-filter predicate (stream-rest s))])))
;(stream-rest s)等价于(force (cdr s))
;注意:stream-rest会force立刻求值
;1.国际惯例,第一步照抄
(stream-head
(stream-rest
(stream-filter prime?
(stream-enum-ab 100 1000000))))
;2.替换(stream-enum-ab 100 1000000)
(stream-head
(stream-rest
(stream-filter prime? (cons 100 ;后面不会被求值,因为delay了
(delay (stream-enum-ab 101 1000000)))
;3.第一个数字不是素数,所以stream-filter需要对流的剩下部分继续寻找
(stream-head
(stream-rest
(stream-filter prime? (force (delay (stream-enum-ab 101 1000000))))))
;这里等价于(stream-filter prime? (stream-enum-ab 101 100000)))
;4.101是素数,所以会得到一个新流
(stream-head
(stream-rest
(cons 101
(delay (stream-filter prime?
(stream-rest (stream-enum-ab 101 1000000)))))))
;这里等价于(force (delay (stream-enum-ab 102 100000))
;5.好吧,我们这里照样抄写一遍
(stream-head
(stream-rest
(cons 101
(delay (stream-filter prime? (stream-enum-ab 102 1000000))))))
;6.第二层的stream-rest脱壳了
(stream-head (force (delay (stream-filter prime?
(stream-enum-ab 102 1000000)))))
(stream-head (stream-filter prime?
(stream-enum-ab 102 100000)))
;7.好吧后面的部分回到了开始,照样参照第2步抄一遍,不同的是从102开始了,而且第二层脱掉了
(stream-head (stream-filter prime?
(const 102 (delay (stream-enum-ab 103 1000000)))))
;8.不是素数stream-filter部分会让后面求值
(stream-head (stream-filter prime?
(stream-enum-ab 103 1000000)))
(stream-head (stream-filter prime?
(cons 103 (delay (stream-enum-ab 104 1000000)))))
;9.是素数构建新流
(stream-head (cons 103 (delay (stream-filter prime?
(stream-enum-ab 104 1000000)))))
;10.神奇的魔法产生了。。。。这里会直接输出103
103
在整个计算序列中,delay和force在不同层级的通用函数之间按需移动,使得整个俄罗斯套娃调用只遍历了5个自然数。
图2说明了流和链表的不同。由于局部惰性求值机制的存在,流范式程序获取了图2中“直通车”式高效运行机制。
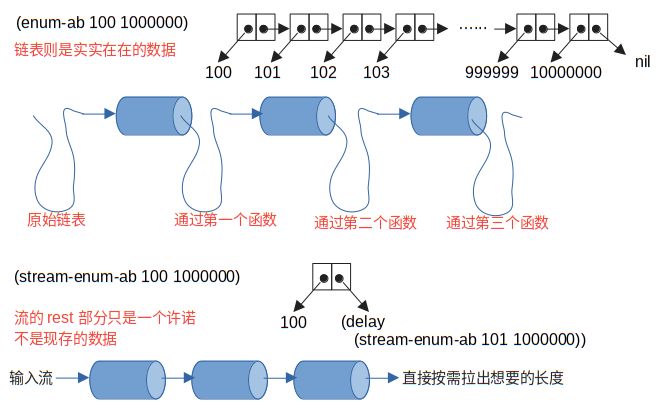
你可以把每个函数想象成一台台机器,数据是一条很长很长的链条。链表版程序是先把链条穿过一台机器,全部拉出来,然后穿过第二个,...。流的实现方法是当链条的头部穿过第一台机器后,立刻让它穿过第二个,而输出端只需要拽着链条的头部往外拉。
3. delay和force函数的实现¶
在图2中,由于局部惰性求值的加入,流并没有显式的写出所有数据。它是一个由“第一个元素”和被delay的“余下部分”的序对。当我们每次执行stream-rest的时候,“余下部分”才会被force求值。虽然delay和force貌似有极大的魔力,但它们的实现却是极其直截了当的。
首先讨论delay, 由于在Lisp或Scheme语言中作为参数的表达式会首先求值(应用序求值)。对于某个表达式exp而言,delay函数需要返回一个保留了exp的逻辑但又不会被立刻求值的东西。很明显,这东西就是lambda表达式,定义如下:
(define delay ;定义delay是一个关于exp的函数
(lambda (exp)
(lambda () exp))) ;它返回一个空参函数,其函数体是exp本身
(delay 5) ;对(delay 5)的求值不会返回5
(lambda () 5) ;而是一个无参的返回5的函数
这样一来,force函数的实现更加显而易见,它的输入参数应该是一个无参函数,返回值是对无参函数的求值。
(define force ;定义froce是一个关于delayed的函数
(lambda (delayed) ;对delayed求值,就直接外面套个括号就好
(delayed))) ;lisp就是这么自然
;我们试一下(force (delay 5))
(force (delay 5))
;等价于下面这样
(force (lambda () 5))
;等价于下面
((lambda () 5))
;无参,直接返回函数体就是了
5
;注意哦,如果f是一个无参函数,那么(f)是函数的值,不能混淆
当然,上面的delay和force还有很多可以优化的地方。比如在有些应用中我们需要多次对同一个delay过的对象求值,这就需要delay程序拥有记忆的能力。如果它是第一次被调用,那么返回exp的原始形式,否则返回已经求值后的简化形式。比如(delay (+ 1 2))第一次调用返回(lambda () (+ 1 2),而第二次则利用记忆直接返回(lambda () 3)。
小贴士:对于一个编程语言而言,拥有lambda匿名函数该是多么必要的事情。
好吧,到目前为止,我们完成了两件事:1)发现了一种用高阶函数写线性易读代码的流模式,它具有很强的通用性;2)局部惰性求值使得流模式拥有常规丐版暴力编程的同阶时间和空间复杂度。
但魔法才刚刚开始,不信往后看。
4. 无穷流¶
考察以下两个奇葩定义,请花10秒钟思考一下,这种可怕的东西居然是能够高效顺利运行的,实在让人不寒而栗:
(define interger-start-from
(lambda (n)
(cons-stream n (integer-start-from (+ n 1)))))
;看到了吗?上面是一个生成[n, 无穷大)的数列的流
;它实际的样子是(cons n (delay integer-start-from-n+1))
(define postive-integers
(interger-start-from 1))
;没错,很合乎逻辑,正整数就是从1开始数到无穷大的数的集合
delay的存在,程序不会进入死循环的无穷递归。这些无穷流完全可以输入到之前的所有算法当中完美工作。
小贴士:你们都知道递归函数,现在开眼界了吧,数据也可以递归。在Lisp的世界里,函数可以是数据,数据也可以是函数。
如果我要对所有的小于100的偶正整数求平方和,那么流模式的代码如下:
(stream-accumulate
+
0
(stream-map
square
(stream-filter
(lambda (x) (< x 100)) ;这里需要给一个匿名函数
(stream-filter
even?
(integer-start-from 1) ;这里是所有的正整数集
))))
同样,我们也可以定义斐波拉契数的无穷流,它描述了所有的斐波拉契数:
(define fibgen
(lambda (fib1 fib2)
(cons-stream a (fibgen fib1 (+ fib1 fib2)))))
(define all-fibs
(fibgen 0 1))
;这里我不显式的写出来,有兴趣的读者可以在纸上推导一下delay是如何作用的
5. 隐式无穷流¶
如果无穷流已经毁掉你的三观,那么更可怕的来了:你可以像用微分方程去描述物理现象那样,用定理的方式隐性定义无穷流。
比如,你可以定义无穷个1组成的一个流。
(define ones (cons-stream 1 ones))
;看起来循环定义吧,可是它完全合法因为它展开的代码是下面这样
(cons 1 (delay ones))
;第一个元素是1,后面的ones因为delay而延迟求值了,不会陷入死循环
add-streams,它返回两个流的逐对元素的和组成的流:(define add-stream
(lambda (s1 s2)
(stream-map + s1 s2)))
;比如两个无限流ones作add-stream,便会生成无穷多个2的流
(define twos
(add-stream ones ones))
;看看下面这个定义正整数的方式,是不是很恐怖?
(define postive-intergers
(cons-stream 1 (add-stream ones postive-integers)))
postive-integer是(cons 1 (delay something)),something又是某个首元素是1的流和ones的相加,过程是:a) 1, something
b) 1, 1+1, something
c) 1, 1+1, 1+1+1, something
d) 1, 1+1, 1+1+1, 1+1+1+1, ....
我们也可以用同样的风格去定义出所有斐波拉契数的无穷流:
(define all-fibs
(cons-stream 0
(cons-stream 1
(add-stream (stream-rest all-fibs)
all-fibs))))
;这种隐式无穷流的推导也留给读者,试试,很有趣的,头皮发麻。
6. 流与科学计算¶
在科学计算中,有很多求函数不动点的迭代方法,比如牛顿法求平方根,用流模式描述的实现如下:
; x1 = (x0 + x / x0) / 2
; 这是平均阻尼牛顿法求根迭代的核心
(define sqrt-improve
(lambda (guess x)
(average guess (/ x guess))))
; 定义了一个牛顿迭代的无穷流
; 这个无穷流里面嵌套了一个所有猜测值的无穷流
(define sqrt-stream
(lambda (x)
(define guess-stream
(cons-stream
1.0
(stream-map
(lambda (guess) (sqrt-improve guess x))
guess-stream)))
guess-stream))
;牛顿迭代变成了打印出这个流里所有元素的过程,当然这个命令会无限的打印下去
(display-stream (sqrt-stream 2))
;如果你定义了一个打印有限个流元素的过程,譬如
(display-stream-n (sqrt-sream 2) 5)
;它的输出是
1.
1.5
1.4166666666665
1.4142156862745
1.4142135623747
delay和force巧妙的实现了逻辑和数据之间的互换,使得我们拥有了使用高阶函数去写流水线式代码的能力。
7. 结论和吐槽¶
再回到一开始的C语言文件流问题。诚然,文件和所有的IO设备都可以抽象为流。但是C语言的文件流实在是一种极其局限的概念。FILE*类型的文件流体现了惰性求值的思想,因为你在fopen一个文件的时候,实际上它只是把读写的位置指向了文件的开头,而并没有把全部的文件读出来。fprint,fscanf,fgetc等函数同样是流水线上的一些机器。
但是,C的文件流本质是“字节流”,FILE*里并不带有类型信息。更广义的流可以是列表的流,树的流,数字的流,函数的流。
由于没有匿名函数的存在,用C语言实现delay函数变得极其困难,你几乎没有办法写出一个C语言版本的无穷流或隐式无穷流。
python里的range(5)和[1,2,3,4,5]也是不同的东西,前者是惰性求值的流,而后者是链表。所以你写for i in range(100000):而不用担心事先生成了一个巨大链表。但python的流很难让我们用流水线的方式构造程序体。你也没有办法用递归定义的方式描述无限个1,编译器会认为你不能用一个未定义的东西去下定义。
通过修改Lisp解释器的求值顺序(变成正则序求值),你可以得到天生惰性求值的新解释器,而不再需要delay函数。但是这么做的代价是牺牲所有应用序求值语言的高效性,每层调用的表达式都会在栈空间展开,最后再进行嵌套规约求值。所以局部的惰性求值能力即可,过犹不及。
最后吐槽: 很多资深程序员真的知道什么叫“流”吗?Java设计模式里面也有个“流模式”,其代码之龌龊,思维之混乱,表达之罗嗦,令人发指。贴在下面,立此存照。
public interface Flow {
public void action();
}
public class VerifyFlow implements Flow {
@Override
public void action() {
System.out.println("审核");
}
}
public class ApplyFlow implements Flow {
@Override
public void action() {
System.out.println("申请");
}
}
public class ApproveFlow implements Flow {
@Override
public void action() {
System.out.println("审批");
}
}
public class Context {
private Flow flow;
public void setFlow(Flow flow) {
this.flow = flow;
}
public void process() {
flow.action();
}
}
public class Test {
public static void main(String[] args) {
Context ctx = new Context();
ctx.setFlow(new ApplyFlow());
ctx.process();
ctx.setFlow(new VerifyFlow());
ctx.process();
ctx.setFlow(new ApproveFlow());
ctx.process();
}
}