解线性方程组的CG和PCG方法

我们讨论的问题是求解线性方程组${\boldsymbol A} {\boldsymbol x} = {\boldsymbol b}$，其中${\boldsymbol A}$对称正定，当然此时解向量${\boldsymbol x}$存在且唯一。当${\boldsymbol A}$的规模非常大时，对其做LU分解或Cholesky分解极其耗时且内存占用巨大，迭代法可能是唯一可选的求解方案。
迭代法分两种：不动点式的静态迭代方法——如雅可比法（Jacobian）、高斯-赛德尔法（Gauss-Seidel），以及Krylov子空间的非静态迭代方法——如共轭梯度法（conjugate gradient，简称CG）。前者仅在${\boldsymbol A}$的主对角严格占优时才保证收敛，后者的应用更为广泛且通常更快。
以下简述CG的原理、算法实现和预条件问题的解法（PCG）。需要说明的是，CG是最基础的非静态迭代法，本文仅是一篇抛砖引玉的入门级介绍，因水平有限，如有错漏，烦请指出，感激不尽。

1. 二次型和梯度法

对于线性方程组的求解问题，考虑经典二次型如下：

$$f(\boldsymbol x) = \frac{1}{2} {\boldsymbol x}^T {\boldsymbol A} {\boldsymbol x} - {\boldsymbol x}^T {\boldsymbol b}$$

当${\boldsymbol A}$为非奇异阵时，$f(\boldsymbol x)$有唯一的全局极小点${\boldsymbol x}^*$满足梯度$\nabla_{\boldsymbol x}f({\boldsymbol x}^*) = 0$。特别的，当${\boldsymbol A}$对称正定时，刚好有：

$$\nabla_{\boldsymbol x}f({\boldsymbol x}^*) = {\boldsymbol A} {\boldsymbol x}^* - {\boldsymbol b} = 0$$

定义残差向量${\boldsymbol r}^*={\boldsymbol b} - {\boldsymbol A} {\boldsymbol x}^*$，它恰好是函数$f(\boldsymbol x)$在点${\boldsymbol x}^*$处的负梯度方向。此时负梯度为0，残差为0，且满足${\boldsymbol A} {\boldsymbol x}^* = {\boldsymbol b}$。
迭代法试图从点${\boldsymbol x}_0$出发，经$k$次迭代后找到${\boldsymbol r}_k = 0$的点，此时${\boldsymbol x}_k$为最优解${\boldsymbol x}^*$。其通用迭代式可写为${\boldsymbol x}_{k+1} = {\boldsymbol x}_{k} + \alpha_k {\boldsymbol p}_{k}$，其中，${\boldsymbol p}_{k}$被称为下降方向（descent direction），$\alpha_k$称为迭代步长。前者规定了下一步朝何处走，后者规定了走多远。在梯度法（最速下降法）里，${\boldsymbol p}_{k} = -\nabla_{\boldsymbol x}f({\boldsymbol x}_k) = {\boldsymbol r}_{k}$。
现在的问题是如何确定${\alpha_k}$。如果视$f(\boldsymbol x_{k+1})$为一个关于${\alpha_k}$的一维函数，其对步长的偏导为0（即$\nabla_{\alpha_k}f({\boldsymbol x}_{k+1}) = 0$）是${\boldsymbol x}_{k+1}$取在函数极小点上的必要条件，此时${\alpha_k}$即为当前下降方向${\boldsymbol p}_k$的最佳步长（一维精确线搜索步长）如下式：

$$\begin{align} \nabla_{\alpha_k} f({\boldsymbol x}_{k+1}) &= [\nabla_{{\boldsymbol x}_{k+1}} f({\boldsymbol x}_{k+1})]^T \nabla_{\alpha_k} {\boldsymbol x}_{k+1} \\ &= - {\boldsymbol r}_{k+1}^T {\boldsymbol p}_{k} = 0\\ \end{align}$$

继续展开得到：

$$\begin{align} {\boldsymbol r}_{k+1}^T {\boldsymbol p}_{k} &= [{\boldsymbol b} - {\boldsymbol A}({\boldsymbol x}_{k} + {\alpha}_{k} {\boldsymbol p}_{k}) ]^T {\boldsymbol p}_{k} \\ &= ({\boldsymbol b} - {\boldsymbol A}{\boldsymbol x}_{k})^T {\boldsymbol p}_{k} - {\alpha}_{k} ({\boldsymbol A} {\boldsymbol p}_{k})^T {\boldsymbol p}_{k} \\ &= {\boldsymbol r}_{k}^T {\boldsymbol p}_{k} - {\alpha}_{k} {\boldsymbol p}_{k}^T {\boldsymbol A} {\boldsymbol p}_{k} = 0 \end{align}$$

很明显，步长应该取：

$${\alpha}_{k} = \frac {{\boldsymbol r}_{k}^T {\boldsymbol p}_{k}} {{\boldsymbol p}_{k}^T {\boldsymbol A} {\boldsymbol p}_{k}}$$

对于梯度法，因为${\boldsymbol p}_{k} = {\boldsymbol r}_{k}$，所以步长可写为：

$${\alpha}_{k} = \frac {{\boldsymbol r}_{k}^T {\boldsymbol r}_{k}} {{\boldsymbol r}_{k}^T {\boldsymbol A} {\boldsymbol r}_{k}}$$

根据以上推导，可给出 算法1（Steepest Descent） ：
(1) 选定${\boldsymbol x}_0$， ${\boldsymbol r}_0 = {\boldsymbol b} - {\boldsymbol A} {\boldsymbol x}_0$，$k := 0$
(2) while $||{\boldsymbol r}_k|| / ||{\boldsymbol r}_0||$ 不够小：
(3)   $k := k+1$，暂存向量${\boldsymbol q} = {\boldsymbol A} {\boldsymbol r}_{k-1}$
(4)   ${\alpha}_{k} = ({\boldsymbol r}_{k-1}^T {\boldsymbol r}_{k-1}) / ({\boldsymbol r}_{k-1}^T {\boldsymbol A} {\boldsymbol r}_{k-1}) = ({\boldsymbol r}_{k-1}^T {\boldsymbol r}_{k-1}) / ({\boldsymbol r}_{k-1}^T {\boldsymbol q})$
(5)   ${\boldsymbol x}_{k} = {\boldsymbol x}_{k-1} + {\alpha}_{k} {\boldsymbol r}_{k-1}$
(6)   ${\boldsymbol r}_{k} = {\boldsymbol b} - {\boldsymbol A} {\boldsymbol x}_{k} = {\boldsymbol r}_{k-1} - {\alpha}_{k} {\boldsymbol q}$（注：避免重复计算）
(7) end while
(8) 输出${\boldsymbol x}_{k}$

算法1的收敛速度和矩阵${\boldsymbol A}$的条件数有关。若条件数定义为最大和最小的特征值之比$\kappa = \lambda_{max} / \lambda_{min}$， 精确解为${\boldsymbol x}^*$，则最差情况下其收敛速率可用下式度量：

$$\frac{f({\boldsymbol x}_k) - f({\boldsymbol x}^*)}{f({\boldsymbol x}_0) - f({\boldsymbol x}^*)} \leq \left( \frac{\kappa - 1}{\kappa + 1} \right)^{2k}$$

也就是说，条件数越大时，残差减小越慢。其原因用几何方式最好理解（见图1），最简单的情况是向量${\boldsymbol x}$只有两行。当条件数很小时（接近1），$f({\boldsymbol x})$的等值线接近正圆。此时无论迭代从何处开始，由于负梯度方向${\boldsymbol r}_k$总是近似指向极小点，使得收敛速度极快。但当条件数很大时，等值线变成了狭窄的椭圆，负梯度方向并非总是指向极小点，较差的初始迭代点会让收敛过程反复震荡。

图1 问题维度为2的简单情况，大条件数可能会导致非常慢的收敛

2. 共轭梯度法

2.1 简单的二维情况

图2 问题维度为2时构建2步收敛的下降方向

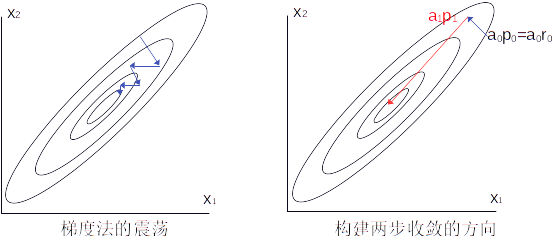
如图2所示，为了改善梯度法的震荡问题，不妨考虑经过一次梯度法迭代${\boldsymbol x}_1={\boldsymbol x}_0 + \alpha_0 {\boldsymbol r}_0$后的情形。如果我们想对${\forall} {\boldsymbol x}_1$一步到位收敛到最优解${\boldsymbol x}^*$，则必然满足：

$$\begin{align} {\boldsymbol x}^* - {\boldsymbol x}_1 &= {\boldsymbol A}^{-1} {\boldsymbol b} - {\boldsymbol A}^{-1} {\boldsymbol A} {\boldsymbol x}_1 \\ &= {\boldsymbol A}^{-1} ({\boldsymbol b} - {\boldsymbol A} {\boldsymbol x}_1) = {\boldsymbol A}^{-1}{\boldsymbol r}_1\\ \end{align}$$

引入向量${\boldsymbol s}_1 = {\boldsymbol x}^* - {\boldsymbol x}_1$（图2右红色箭头所示）。不难看出，由于负梯度方向是${\boldsymbol r}_1$，海塞矩阵是${\boldsymbol A}$，向量${\boldsymbol s}_1$其实就是牛顿法的下降方向。也就是说，不论上一次如何迭代到当前点，我们希望构建一个与牛顿方向${\boldsymbol s}_1$平行的下降方向，使其能一步收敛到${\boldsymbol x}^*$。

小贴士：对于线性二次型目标函数，牛顿法是一步收敛的。

当然，我们不想对${\boldsymbol A}$求逆，否则还折腾什么迭代法？所以首先要考虑和${\boldsymbol s}_1$平行的下降方向${\boldsymbol p}_1$有什么样的性质(这里${\boldsymbol s}_1 = \alpha_1 {\boldsymbol p}_1$)。考虑上一次迭代的修正量${\boldsymbol s}_0={\boldsymbol x}_1 - {\boldsymbol x}_0$，做以下变换：

$$\begin{align} {\boldsymbol s}_0^T {\boldsymbol A} {\boldsymbol s}_1 &= \alpha_0 {\boldsymbol p}_0^T {\boldsymbol A} {\boldsymbol s}_1 = \alpha_0 {\boldsymbol p}_0^T {\boldsymbol A} {\boldsymbol A}^{-1} {\boldsymbol r}_1\\ &= \alpha_0 {\boldsymbol p}_0^T {\boldsymbol r}_1\\ \end{align}$$

根据之前最速下降法介绍的步长择优条件(${\boldsymbol r}_{k+1}^T {\boldsymbol p}_k = 0$)，上式应为0，即${\boldsymbol s}_0^T {\boldsymbol A} {\boldsymbol s}_1 = 0$。由于步长是标量，进一步简化可以得到${\boldsymbol p}_0^T {\boldsymbol A} {\boldsymbol p}_1 = 0$。也就是说，对于图2的简单问题，平行于牛顿方向${\boldsymbol s}_1$的下降方向${\boldsymbol p}_1$必然和上一步的下降方向${\boldsymbol p}_0$关于矩阵${\boldsymbol A}$共轭。
满足共轭条件的${\boldsymbol p}_1$有无数个，只需取一个即可。当前我们已知${\boldsymbol p}_0$和${\boldsymbol r}_1$，其中${\boldsymbol r}_1$为最速下降方向，沿${\boldsymbol p}_0$的极小已在上次迭代完成，不妨取新方向为${\boldsymbol p}_0$和${\boldsymbol r}_1$的线性组合${\boldsymbol p}_1 = {\boldsymbol r}_1 + \beta_1 {\boldsymbol p}_0$，代入共轭条件后得：

$${\boldsymbol p}_0 ^T {\boldsymbol A} {\boldsymbol p}_1 = {\boldsymbol p}_0 ^T {\boldsymbol A} {\boldsymbol r}_1 + \beta_1 {\boldsymbol p}_0 ^T {\boldsymbol A} {\boldsymbol p}_0 = 0$$

故，$\beta_1$满足：

$$\beta_1 = - \frac {{\boldsymbol r}_1 ^T {\boldsymbol A} {\boldsymbol p}_0} {{\boldsymbol p}_0 ^T {\boldsymbol A} {\boldsymbol p}_0}$$

上式是利用${\boldsymbol r}_1$（负梯度）、${\boldsymbol p}_0$和共轭性${\boldsymbol p}_0 ^T {\boldsymbol A} {\boldsymbol p}_1=0$构建的，因此这样的迭代法也被称为共轭梯度法（CG），它对于二维问题，最多两次迭代即可收敛。

2.2 推广到高维

当推广到$n$维问题之后，共轭梯度法不再具有最多两次迭代收敛的性质（实际上是$n$次收敛），此时第$k$次迭代的下降方向${\boldsymbol p}_k$可用之前的所有下降方向构建：

$${\boldsymbol p}_k = {\boldsymbol r}_k + \sum_{i=0}^{k-1}{\beta_{ki} {\boldsymbol p}_i }$$

且任意两个不同下降方向${\boldsymbol p}_i$和${\boldsymbol p}_j$之间互相关于${\boldsymbol A}$共轭，即${\boldsymbol p}_i^T {\boldsymbol A} {\boldsymbol p}_j = 0$：

$$\begin{align} {\boldsymbol p}_i^T {\boldsymbol A} {\boldsymbol p}_j &= {\boldsymbol r}_i^T {\boldsymbol A} {\boldsymbol p}_j + \sum_{i=0}^{k-1}{\beta_{ki} {\boldsymbol p}_i {\boldsymbol A} {\boldsymbol p}_j} \\ &= {\boldsymbol r}_i^T {\boldsymbol A} {\boldsymbol p}_j + \beta_{ij} {\boldsymbol p}_j^T {\boldsymbol A} {\boldsymbol p}_j = 0\\ \end{align}$$

上式消除求和符号是利用了$i \neq j$时的共轭性， 从而可解出高维情况下一般形式的$\beta$表达式：

$$\beta_{ij} = - \frac {{\boldsymbol r}_i^T {\boldsymbol A} {\boldsymbol p}_j} {{\boldsymbol p}_j^T {\boldsymbol A} {\boldsymbol p}_j}$$

在引出算法之前，我们需要避免对之前所有迭代的下降方向求和，以减小计算开销。首先根据共轭性得到三个推论：

[推论1] ：
考虑$\forall j > i$，计算${\boldsymbol p}_i^T {\boldsymbol r}_j$，利用共轭性可得到：

$${\boldsymbol p}_i^T {\boldsymbol r}_j = {\boldsymbol p}_i^T {\boldsymbol A}({\boldsymbol x}^* - {\boldsymbol x}_j) = - {\boldsymbol p}_i^T {\boldsymbol A} \sum_{k=0}^{n-1}{\alpha_{k} {\boldsymbol p}_k } =- \sum_{k=j}^{n-1}{\alpha_{k} {\boldsymbol p}_i^T {\boldsymbol A} {\boldsymbol p}_k }$$

其中，$n$为最终收敛到最优点${\boldsymbol p}^*$的迭代次数，由于共轭性，求和项为0。即对$\forall j > i$都存在${\boldsymbol p}_i^T {\boldsymbol r}_j = 0$。 这表明当前迭代残差向量与之前迭代的所有下降方向正交。

[推论2] ：
取$\forall j > i$，求${\boldsymbol p}_i$和${\boldsymbol r}_j$的内积，得：

$${\boldsymbol p}_i^T {\boldsymbol r}_j = {\boldsymbol r}_i^T {\boldsymbol r}_j + \sum_{k=0}^{i-1}{\beta_{ik} {\boldsymbol p}_k^T {\boldsymbol r}_j}$$

利用推论1可知，上式中所有${\boldsymbol p}_i^T {\boldsymbol r}_j$和${\boldsymbol p}_k^T {\boldsymbol r}_j$均为0，从而${\boldsymbol r}_i^T {\boldsymbol r}_j = 0$。也就是说CG的当前迭代残差向量与之前所有迭代的残差向量都正交。

[推论3] ：
考虑精确线搜索步长通式$\alpha_k = {\boldsymbol p}_i^T {\boldsymbol r}_i / ({\boldsymbol p}_i^T {\boldsymbol A} {\boldsymbol p}_i^T)$的分子部分：

$${\boldsymbol p}_i^T {\boldsymbol r}_i = {\boldsymbol r}_i^T {\boldsymbol r}_i + \sum_{k=0}^{i-1}{\beta_{ik} {\boldsymbol p}_k^T {\boldsymbol r}_i}$$

由推论1可知上式求和项为0， 故CG每次迭代的步长也可写为$\alpha_k = {\boldsymbol r}_i^T {\boldsymbol r}_i / ({\boldsymbol p}_i^T {\boldsymbol A} {\boldsymbol p}_i^T)$。

有了以上三个推论，CG迭代式即可逐步简化，首先考虑以下关系：

$${\boldsymbol r}_i^T {\boldsymbol r}_{j+1} = {\boldsymbol r}_i^T ({\boldsymbol r}_j - \alpha_j {\boldsymbol A} {\boldsymbol p}_j) = {\boldsymbol r}_i^T {\boldsymbol r}_j - \alpha_j {\boldsymbol r}_i^T {\boldsymbol A} {\boldsymbol p}_j$$

即

$$\alpha_j {\boldsymbol r}_i^T {\boldsymbol A} {\boldsymbol p}_j = {\boldsymbol r}_i^T {\boldsymbol r}_{j} - {\boldsymbol r}_i^T {\boldsymbol r}_{j+1}$$

利用推论1和推论2，得到：

$${\boldsymbol r}_i^T {\boldsymbol A} {\boldsymbol p}_j = \left\{ \begin{array}{**lr**} {\boldsymbol r}_i^T {\boldsymbol r}_i/{\alpha_i}, \quad if \quad i=j, {\boldsymbol r}_i^T {\boldsymbol r}_{j+1} = 0 &\\ - {\boldsymbol r}_i^T {\boldsymbol r}_i/{\alpha_{i-1}}, \quad if \quad i=j+1, {\boldsymbol r}_i^T {\boldsymbol r}_{j} = 0 &\\ 0, \quad otherwise \end{array} \right.$$

利用上面的性质可简化$\beta_{ij}$如下：

$$\beta_{ij} = - \frac {{\boldsymbol r}_i^T {\boldsymbol A} {\boldsymbol p}_j} {{\boldsymbol p}_j^T {\boldsymbol A} {\boldsymbol p}_j} = \left\{ \begin{array}{**lr**} \frac{1}{\alpha_{i-1}} \frac{{\boldsymbol r}_i^T {\boldsymbol r}_i}{{\boldsymbol p}_j^T {\boldsymbol A} {\boldsymbol p}_j} = \frac{{\boldsymbol r}_i^T {\boldsymbol r}_i}{{\boldsymbol p}_{i-1}^T {\boldsymbol r}_{i-1}} , \quad if \quad j=i-1 &\\ 0, \quad if \quad j < i-1 \end{array} \right.$$

只考虑$j = i-1$的情况，利用推论2可得到${\boldsymbol p}_{i-1}^T {\boldsymbol r}_{i-1} = {\boldsymbol r}_{i-1}^T {\boldsymbol r}_{i-1}$，此时$\beta_{ij}$可进一步简化为：

$$\beta_{ij} = \frac{{\boldsymbol r}_i^T {\boldsymbol r}_i} {{\boldsymbol r}_{i-1}^T {\boldsymbol r}_{i-1}}$$

此时CG的下降方向可简化为：

$$\begin{align} {\boldsymbol p}_k &= {\boldsymbol r}_k + \sum_{i=0}^{k-1}{\beta_{ki} {\boldsymbol p}_i }\\ &= {\boldsymbol r}_k + {\beta_{k,k-1} {\boldsymbol p}_{k-1} } + \sum_{i=0}^{k-2}{\beta_{ki} {\boldsymbol p}_i }\\ &= {\boldsymbol r}_k + {\beta_{k,k-1} {\boldsymbol p}_{k-1} }\\ \end{align}$$

不妨令$\beta_k = \beta_{k,k-1}$，CG下降方向为${\boldsymbol p}_k = {\boldsymbol r}_k + {\beta_k {\boldsymbol p}_{k-1} }$。化简后的版本无需保存所有之前的迭代下降方向，极大减小了算法消耗。

根据以上，可以给出 算法2（CG） ：
(1) 选定${\boldsymbol x}_0$， ${\boldsymbol r}_0 = {\boldsymbol b} - {\boldsymbol A} {\boldsymbol x}_0$，$k := 0$， ${\boldsymbol p} := {\boldsymbol r}_0$, ${\boldsymbol r} := {\boldsymbol r}_0$，${\boldsymbol x} := {\boldsymbol x}_0$
(2) $\gamma := {\boldsymbol r}^T{\boldsymbol r}$， $\gamma_0 := \gamma$
(3) while $\sqrt{(\gamma / \gamma_0)}$ 不够小：
(4)   $k := k+1$
(5)   ${\boldsymbol q} := {\boldsymbol A} {\boldsymbol r}_{k-1} = {\boldsymbol A} {\boldsymbol p}$
(6)   $\alpha := \alpha_k = {\boldsymbol r}^T {\boldsymbol r} / ({\boldsymbol p}^T {\boldsymbol q})$
(7)   ${\boldsymbol x} := {\boldsymbol x} + \alpha {\boldsymbol p}$
(8)   ${\boldsymbol r} := {\boldsymbol r} - \alpha {\boldsymbol q}$
(9)   $\gamma_1 := \gamma$， $\gamma := {\boldsymbol r}^T{\boldsymbol r}$， $\beta := \gamma / \gamma_1$
(10)   ${\boldsymbol p} := {\boldsymbol r} + \beta {\boldsymbol p}$
(11) end while
(12) 输出${\boldsymbol x} = {\boldsymbol x}_{k}$

小贴士： 二维问题CG最多两次迭代即可收敛。对于$n$维问题，CG最多需要$n$次迭代即可收敛，这种性质叫做CG的二次截止性。可以不严谨的想象为：最差的情况是每次找到$n$维空间的一个2维子空间内的极小点投影。

3. 预条件共轭梯度法

当问题的维度$n$非常大时，二次截止性并不能保证算法在可接受的时间内收敛。若矩阵${\boldsymbol A}$的条件数非常大，求解一个转换的小条件数问题会使算法提速。引入矩阵${\boldsymbol M}$，如果${\boldsymbol M}^{-1}{\boldsymbol A}$的条件数很小（比如接近于1），那么以下问题的求解会非常快：

$${\boldsymbol M}^{-1}{\boldsymbol A}{\boldsymbol x} = {\boldsymbol M}^{-1}{\boldsymbol b}$$

很明显${\boldsymbol M} \approx {\boldsymbol A}$是较好的情况，此时新矩阵${\boldsymbol M}^{-1}{\boldsymbol A}$的条件数接近于1（对应图1左边的正圆），这一过程被称为预条件（preconditioning），矩阵${\boldsymbol M}$也被称为预条件阵。

小贴士： 几何上的解释是把原问题的椭圆型等值线变换到尽量正圆的新问题中求解，故此过程也被称为圆化（rounding）。当然，高维情况是个广义椭球。

但新矩阵${\boldsymbol M}^{-1}{\boldsymbol A}$并不一定保证对称正定，这样常规CG方法就没法用来解新方程了。因此需要通过一个特别的技巧绕过这个棘手问题。对于任意的对称正定预条件阵${\boldsymbol M}$，一定存在（且不唯一）某个可逆矩阵${\boldsymbol E}$满足${\boldsymbol E}{\boldsymbol E}^T = {\boldsymbol M}$。 虽然${\boldsymbol E}$可以用Choleksy分解获得，但我们这里并不需要指定它是什么，它只是一个推导的中间变量，最终会被化简消除。
若${\boldsymbol v}$是矩阵${\boldsymbol M}^{-1}{\boldsymbol A}$的一个特征值为$\lambda$的特征向量。则有：

$$\begin{align} & {\boldsymbol M}^{-1}{\boldsymbol A}{\boldsymbol v} = \lambda {\boldsymbol v} \\ & {\boldsymbol E}^T {\boldsymbol M}^{-1}{\boldsymbol A}{\boldsymbol v} = \lambda {\boldsymbol E}^T {\boldsymbol v} = {\boldsymbol E}^T {\boldsymbol E}^{-T} {\boldsymbol E}^{-1} {\boldsymbol A}{\boldsymbol v} = {\boldsymbol E}^{-1} {\boldsymbol A}{\boldsymbol v} = {\boldsymbol E}^{-1} {\boldsymbol A}{\boldsymbol E}^{-T}{\boldsymbol E}^{T}{\boldsymbol v} \\ \end{align}$$

这也就是说，我们把原方程两边同时左乘${\boldsymbol E}^{T}$后，系数矩阵${\boldsymbol M}^{-1}{\boldsymbol A}$可转换为${\boldsymbol E}^{-1} {\boldsymbol A}{\boldsymbol E}^{-T}{\boldsymbol E}^{T}$。不妨称对称正定矩阵${\boldsymbol E}^{-1} {\boldsymbol A}{\boldsymbol E}^{-T}$为${\boldsymbol P}$，根据上式，${\boldsymbol P}$和${\boldsymbol M}^{-1} {\boldsymbol A}$具有同样的特征值（条件数一样），但它的特征向量变成了${\boldsymbol E}^T {\boldsymbol v}$。原预条件问题的两边同时左乘${\boldsymbol E}^T$后，新方程可改写为：

$$\begin{align} & {\boldsymbol E}^T {\boldsymbol M}^{-1}{\boldsymbol A}{\boldsymbol x} = {\boldsymbol E}^T {\boldsymbol M}^{-1} {\boldsymbol b} \\ & {\boldsymbol E}^{-1} {\boldsymbol A}{\boldsymbol E}^{-T}{\boldsymbol E}^{T}{\boldsymbol v} = {\boldsymbol E}^T {\boldsymbol E}^{-T} {\boldsymbol E}^{-1} {\boldsymbol b} \\ & {\boldsymbol P} {\boldsymbol E}^{T}{\boldsymbol x} = {\boldsymbol E}^{-1} {\boldsymbol b} \\ & {\boldsymbol P} \hat{\boldsymbol x} =\hat{\boldsymbol b}\\ \end{align}$$

其中，${\boldsymbol P}$为一个小条件数的对称正定矩阵，$\hat{\boldsymbol x} = {\boldsymbol E}^{T}{\boldsymbol x}$， $\hat{\boldsymbol b} = {\boldsymbol E}^{-1}{\boldsymbol b}$。

小贴士： 看到这里你可能会皱眉，如果${\boldsymbol E}$是对${\boldsymbol M}$的完全分解（如cholesky），我都已经完全分解了，还需要搞个鸡毛的CG迭代啊？但请注意，这里的${\boldsymbol E}$只是一个中间变量，一会我们需要把他消除，使得计算中只存在对${\boldsymbol M}$的操作。

首先写出关于 预条件转换后 的方程${\boldsymbol P} \hat{\boldsymbol x} =\hat{\boldsymbol b}$的 无预条件CG 迭代式：

$$\begin{align} & \hat{\boldsymbol p}_0 = \hat{\boldsymbol r}_0 = {\boldsymbol E}^{-1} {\boldsymbol b} - {\boldsymbol E}^{-1} {\boldsymbol A}{\boldsymbol E}^{-T}{\boldsymbol E}^{T}{\boldsymbol x}_0 = {\boldsymbol E}^{-1} ({\boldsymbol b} - {\boldsymbol A} {\boldsymbol x}_{0})\\ & \hat{\alpha_k} = \hat{\boldsymbol r}_k^{T} \hat{\boldsymbol r}_k / (\hat{\boldsymbol p}_k^{T} {\boldsymbol E}^{-1} {\boldsymbol A}{\boldsymbol E}^{-T} \hat{\boldsymbol p}_k) \\ & \hat{\boldsymbol x}_{k+1} = \hat{\boldsymbol x}_{k} + \hat{\alpha_k} \hat{\boldsymbol p}_k \\ & \hat{\boldsymbol r}_{k+1} = \hat{\boldsymbol r}_{k} - \hat{\alpha_k} {\boldsymbol E}^{-1} {\boldsymbol A}{\boldsymbol E}^{-T} \hat{\boldsymbol p}_k \\ & \hat{\beta}_{k+1} = \hat{\boldsymbol r}_{k+1}^{T} \hat{\boldsymbol r}_{k+1} / (\hat{\boldsymbol r}_k^{T} \hat{\boldsymbol r}_k) \\ & \hat{\boldsymbol p}_{k+1} = \hat{\boldsymbol r}_{k+1} + \hat{\beta}_{k+1} \hat{\boldsymbol p}_k \end{align}$$

要把上式变换到对${\boldsymbol x}$的迭代格式，需利用关系式${\boldsymbol x}_k = {\boldsymbol E}^{-T} \hat{\boldsymbol x}_{k}$ (同理${\boldsymbol p}_k = {\boldsymbol E}^{-T} \hat{\boldsymbol p}_{k}$)，$\hat{\boldsymbol r}_k = {\boldsymbol E}^{-1} {\boldsymbol r}_k$从而有：

$$\begin{align} & {\boldsymbol p}_0 = {\boldsymbol E}^{-T} \hat{\boldsymbol r}_0 = {\boldsymbol M}^{-1} {\boldsymbol r}_0 \\ & {\boldsymbol x}_{k+1} = {\boldsymbol E}^{-T}\hat{\boldsymbol x}_{k+1} = {\boldsymbol E}^{-T}\hat{\boldsymbol x}_{k} + \hat{\alpha_k} {\boldsymbol E}^{-T} \hat{\boldsymbol p}_k = {\boldsymbol x}_{k} + {\alpha_k} {\boldsymbol p}_{k}\\ & {\alpha_k} = \hat{\alpha_k} = \frac{ \hat{\boldsymbol r}_k^{T} \hat{\boldsymbol r}_k } { \hat{\boldsymbol p}_k^{T} {\boldsymbol E}^{-1} {\boldsymbol A}{\boldsymbol E}^{-T} \hat{\boldsymbol p}_k } = \frac { {\boldsymbol r}_k^{T} {\boldsymbol E}^{-T} {\boldsymbol E}^{-1} {\boldsymbol r}_k } { {\boldsymbol p}_k^{T} {\boldsymbol E} {\boldsymbol E}^{-1} {\boldsymbol A}{\boldsymbol E}^{-T} {\boldsymbol E}^{T} {\boldsymbol p}_k } = \frac { {\boldsymbol r}_k^{T} {\boldsymbol M}^{-1} {\boldsymbol r}_k } { {\boldsymbol p}_k^{T} {\boldsymbol A} {\boldsymbol p}_k }\\ & {\boldsymbol r}_{k+1} = {\boldsymbol E} \hat{\boldsymbol r}_{k+1} = {\boldsymbol E} \hat{\boldsymbol r}_{k} - \hat{\alpha_k} {\boldsymbol E} {\boldsymbol E}^{-1} {\boldsymbol A}{\boldsymbol E}^{-T} {\boldsymbol E}^{T} \hat{\boldsymbol p}_k = {\boldsymbol r}_{k} - {\alpha_k} {\boldsymbol A}{\boldsymbol p}_k\\ & {\boldsymbol p}_{k+1} = {\boldsymbol E}^{-T} \hat{\boldsymbol p}_{k+1} = {\boldsymbol E}^{-T} \hat{\boldsymbol r}_{k+1} + \hat{\beta}_{k+1} {\boldsymbol E}^{-T} \hat{\boldsymbol p}_k = {\boldsymbol M}^{-1} {\boldsymbol r}_{k+1} + \beta_{k+1} {\boldsymbol p}_{k+1} \\ & {\beta}_{k+1} = \hat{\beta}_{k+1} = \frac { \hat{\boldsymbol r}_{k+1}^{T} \hat{\boldsymbol r}_{k+1} } { \hat{\boldsymbol r}_k^{T} \hat{\boldsymbol r}_k } = \frac { {\boldsymbol r}_{k+1}^{T} {\boldsymbol E}^{-T} {\boldsymbol E}^{-1} {\boldsymbol r}_{k+1} } { {\boldsymbol r}_k^{T} {\boldsymbol E}^{-T} {\boldsymbol E}^{-1} {\boldsymbol r}_k } = \frac { {\boldsymbol r}_{k+1}^{T} {\boldsymbol M}^{-1} {\boldsymbol r}_{k+1} } { {\boldsymbol r}_k^{T} {\boldsymbol M}^{-1} {\boldsymbol r}_k } \end{align}$$

“妙啊”！我不禁高喊。对${\boldsymbol x}_k$的直接迭代产生了一个奇迹，${\boldsymbol E}$的显式形式不再重要。对于任何对称正定的预条件阵${\boldsymbol M}$，无论${\boldsymbol M}^{-1}{\boldsymbol A}$是否对称，均可用上式直接对${\boldsymbol x}_k$进行迭代求解（PCG）。

但仍有一个遗留问题，如何求${\boldsymbol M}^{-1}$？当然有一种土豪的办法是对${\boldsymbol M}$进行cholesky分解，但这样分解需要的时间都足够直接解出${\boldsymbol A}{\boldsymbol x}={\boldsymbol b}$了。所以实用中往往需要快速近似${\boldsymbol M}^{-1}$和任意向量${\boldsymbol v}$的乘积。
举个栗子，如果${\boldsymbol M}$是一个稀疏阵，那么我们可以利用不完全分解技术（如ILU和ICC），构建一个稀疏下三角矩阵${\boldsymbol L}$和一个稀疏上三角矩阵${\boldsymbol U}$，使得${\boldsymbol L}{\boldsymbol U} = \hat{\boldsymbol M} \approx {\boldsymbol M}$。进而利用稀疏三角回代技术快速近似${\boldsymbol M}^{-1}{\boldsymbol v}$。 注意，经过不完全分解的近似后，预条件阵实际上是$\hat{\boldsymbol M}$，而非${\boldsymbol M}$。

小贴士： 无需担心${\boldsymbol L}$和${\boldsymbol U}$是否互为转置，因为矩阵${\boldsymbol L}{\boldsymbol U}$是${\boldsymbol M}$的对称正定近似，那么正如本节一开始所言，它必然存在一个分解使得${\boldsymbol L}{\boldsymbol U} = {\boldsymbol E}{\boldsymbol E}^T$。

综上，我们可以提出 算法3 (PCG)：
(1) 选定${\boldsymbol x}_0$，${\boldsymbol M}$， ${\boldsymbol r}_0 = {\boldsymbol b} - {\boldsymbol A} {\boldsymbol x}_0$
(2) $k := 0$， ${\boldsymbol z} := {\boldsymbol M}^{-1} {\boldsymbol r}_0$, ${\boldsymbol r} := {\boldsymbol r}_0$，${\boldsymbol x} := {\boldsymbol x}_0$， ${\boldsymbol p} := {\boldsymbol z}$
(3) $\gamma := {\boldsymbol r}^T{\boldsymbol r}$， $\gamma_0 := \gamma$
(4) while $\sqrt{(\gamma / \gamma_0)}$ 不够小：
(5)   $k := k+1$
(6)   ${\boldsymbol q} := {\boldsymbol A} {\boldsymbol r}_{k-1} = {\boldsymbol A} {\boldsymbol p}$
(7)   $\delta = {\boldsymbol r}^T {\boldsymbol z}$
(8)   $\alpha := \alpha_k = \delta / ({\boldsymbol p}^T {\boldsymbol q})$
(9)   ${\boldsymbol x} := {\boldsymbol x} + \alpha {\boldsymbol p}$
(10)   ${\boldsymbol r} := {\boldsymbol r} - \alpha {\boldsymbol q}$
(11)   ${\boldsymbol z} := {\boldsymbol M}^{-1} {\boldsymbol r}$
(12)   $\delta_1 := \delta$， $\delta := {\boldsymbol r}^T{\boldsymbol z}$， $\beta := \delta / \delta_1$，$\gamma := {\boldsymbol r}^T {\boldsymbol r}$
(13)   ${\boldsymbol p} := {\boldsymbol r} + \beta {\boldsymbol p}$
(14) end while
(15) 输出${\boldsymbol x} = {\boldsymbol x}_{k}$

4. 总结

以上讨论的是线性二次型问题，限定了矩阵${\boldsymbol A}$对称正定的情况，如果${\boldsymbol A}$不对称，则需要转换为最小二乘形式${\boldsymbol A}^T{\boldsymbol A}{\boldsymbol x} = {\boldsymbol A}^T {\boldsymbol b}$求解。CG的其他变种方法（如BICG和BICGStab）可直接用于这种不对称问题。
在地球物理反演中，由于正演过程往往是非线性函数，反演目标函数是非线性最小二乘形式。此时，CG方法也可应用，不同点在于负梯度方向不是${\boldsymbol r}_k$而变为$-{\boldsymbol g}_k$，${\alpha}_k$不再能直接求得，而需对当前迭代的线性子问题近似得到，且这样得到的${\alpha}_k$不再保证目标函数下降（所以需要不精确线搜索）。另外，${\beta}_k$也要进行修改（有很多方式），篇幅所限，不再赘述。这样的CG方法被称为非线性共轭梯度(NLCG)。
PCG问题的推导过程非常巧妙，一个不正定的问题一通骚操作后转换成了正定问题，而且绕回去之后基本没增加什么运算量。我只能说，这很牛逼。
加速一个最优化方法的关键点在于条件数，CG方向和预条件都是从rounding的思想出发。如果联系牛顿法去思考可能发现一个神奇现象：牛顿法的本质在于用${\boldsymbol A}$范数去缩放原大条件数问题的2范数梯度，得到${\boldsymbol A}$范数的最速下降方向（牛顿方向）。而CG则构建${\boldsymbol p}_{k-1}^T {\boldsymbol A} {\boldsymbol p}_k$的度量，我隐隐觉得CG下降方向是一种牛顿方向的不动点迭代。

小贴士：NLCG失去了线性CG的二次截至性。

5. 致谢

写本文的缘由是和喻国博士交流CG方法被问卡壳了，CG这玩意自己很早就用，并且由于其效果有限，一直不求甚解，很多理解不够深刻。这回好好重新推导了一次，收获颇大。感谢喻博士对细节的认真态度，否则我都不知道自己对CG的理解一直有偏差。
本文的推导和原理论述借鉴了浙江大学赵海亮博士的公开笔记http://hliangzhao.me/math/CG.pdf，非常感谢赵博士的总结和分享。